Hey, I'm trying to find out if I have enough threads to withstand a force caused by pressure.
The hub is made of duplex steel and the threaded cylinder is of Titanium Grade 2.
The threads are 1/2'' BSP Pipe threads.
Just a quick sketch:
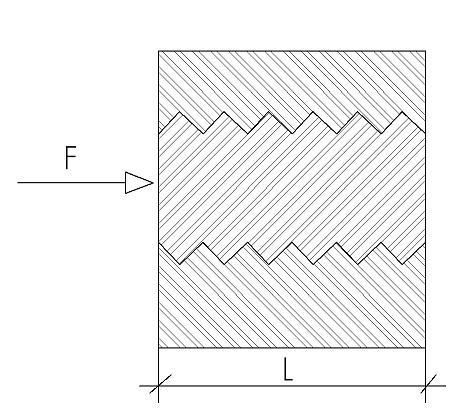
Is it enough to calculate the shear stress :
tau = F/pi*di*L and just compare it to the shear strength of Ti
Or do I have to take in account the amount of stress every thread takes?
All comments are appreciated, thanks.
The hub is made of duplex steel and the threaded cylinder is of Titanium Grade 2.
The threads are 1/2'' BSP Pipe threads.
Just a quick sketch:

Is it enough to calculate the shear stress :
tau = F/pi*di*L and just compare it to the shear strength of Ti
Or do I have to take in account the amount of stress every thread takes?
All comments are appreciated, thanks.
