Continue to Site

Eng-Tips is the largest engineering community on the Internet

Intelligent Work Forums for Engineering Professionals

Register Log in
  • Congratulations waross on being selected by the Eng-Tips community for having the most helpful posts in the forums last week. Way to Go!

Force required to lift one end of infinitely long beam 1

Status
Not open for further replies.
tomecki

tomecki

Mechanical
Aug 18, 2014
18
CA
I'm trying to figure out the force required to lift up one end of a long pipe by 2m. The pipe is long enough that the entire length of it will not lift off the ground. It will bend under it's own weight and become tangent with the ground at some unknown point away from the end.

I tried to model this using various beam formulas but I end up with two unknowns (the force on one end and the length that lifts off) and can't solve them.


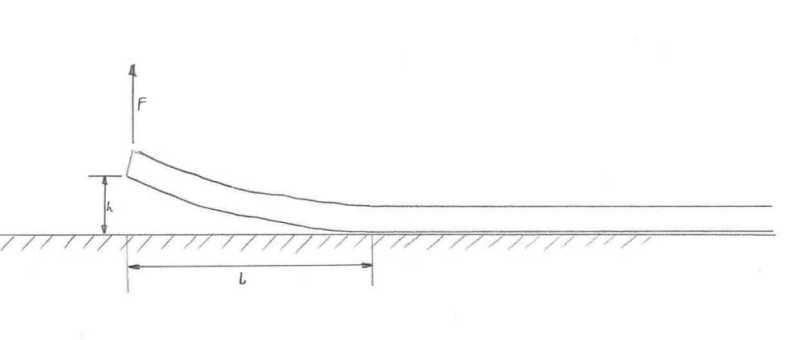
Pipe_lift_bsewhp.jpg
 
Replies continue below

Recommended for you

Sort by date Sort by votes
It's going to depend on the stiffness of what you are lifting. The stiffer it is: the more you are going to pick up.
 
Upvote 0 Downvote
I think you need to go back to old fashioned iteration where you guess at the beam length, solve for F knowing the tip deflection and accounting for self weight, and then check force balance as F and the total self weight of the lifted beam will cancel each other out just as the pipe touches the ground. Re-iterate until the forces balance.
 
Upvote 0 Downvote
If you can lift it an infinite height, the force would be infinite... or at least infinite/2.

Dik
 
Upvote 0 Downvote
I'm not sure if this'll get you anywhere, but do an energy calc ...
the external work done by F = the internal strain energy in the pipe (consider as a cantilever, length L).

This will give you a relationship in terms of the pipe's stiffness ... the stiffer the pipe, the longer L.

another day in paradise, or is paradise one day closer ?
 
Upvote 0 Downvote
I'm not sure if this'll get you anywhere, but do an energy calc ...
Click to expand...

Why do that? I could knock this out in 5 minutes on STAAD. Just a beam on compression only springs.
 
Upvote 0 Downvote
if you're FEMing it, then you know the stiffness.

maybe the OP doesn't have access to a FEA ?

many ways to skin cats ...
(cats like none of them)

another day in paradise, or is paradise one day closer ?
 
Upvote 0 Downvote
I seriously think that doing an iteration in excel would be the quickest and easiest. Using solver or goalseek would make short work of the problem.
 
Upvote 0 Downvote
How accurate do you need to be? Do you consider shear deformation? Do you include the distributed linear weight of the pipe to resist the force, or ignore it by assuming F >> weight? You need to know the modulus of elasticity of the pipe, the moment of inertia, and maybe some other things if you want to get super accurate. I would use singularity functions to solve this myself with a quick guess and check to hone in on the solution. The pipe is a cantilever with the fixed end location at the point where the deformation equals zero.

Juston Fluckey, SE, PE, AWS CWI
Engineering Consultant
 
Upvote 0 Downvote
In addition, the shear/moment at the "fixed" end cannot exceed the allowable shear/moment of the pipe or you will buckle it before you get the height you want. You deflection curve would look much different if that happened!

Juston Fluckey, SE, PE, AWS CWI
Engineering Consultant
 
Upvote 0 Downvote
F has to equal the weight of the pipe of of length L.
Click to expand...

Actually no because you are creating a couple that will result in a increase in bearing pressure at the point where zero contact ends that will be in excess of its self weight. So by equilibrium, more will be picked up than the applied force. (How much will vary based on stiffness.)

 
Upvote 0 Downvote
Thanks for the suggestions.

I assumed that F = 1/2 weight of pipe of length l. Then solved for l using beam formulas. I did one calc using the cantilever beam model and one using the simply supported beam model. The moment in the pipe at the location where it lifts off the ground must be small because both calcs gave very similar results.

 
Upvote 0 Downvote
I assume your simply supported model meant that the weight is support be F and by the reaction at the end of the pipe ?

by assuming F = wt/2, you are driving the cantilever solution to be close to the SS model (F = wt/2 acting at distance L reacts the wt acting at L/2 so the fixed end moment is small. F = wt/2 is possibly the limit of a rigid pipe.



another day in paradise, or is paradise one day closer ?
 
Upvote 0 Downvote
Note that there are two different approaches above. If you treat the ground as compression-only springs, that's good, but it also means deflection is not zero beyond the first contact point, and that the slope is not zero at the first contact point. IE, it's a different solution than treating it as a cantilever, which assumes that at some point, it must be "fixed".

What I'd suggest for a theoretical solution- treat it as two beams, the "lifted" part being a conventional beam, the "contacted" part being a beam on elastic foundation. The "right" length is the one that shows zero deflection at the assumed contact point. If you get any "suction" beyond that point, the method fails, although it would show that beyond the first contact point is a point that lifts off the ground, which seems counter-intuitive.
 
Upvote 0 Downvote
I don't think anyone has mentioned the strength of the pipe. There is no guarantee that the end of the pipe can be lifted as much as 2m without yielding the pipe.

BA
 
Upvote 0 Downvote
That's a cute analytical problem (if we ignore shear and buckling effects), did you solve it? However I suspect the stiffness of the ground is crucial. But yeah, FEA, then plug the answer back into a hand calc as a check.

Cheers

Greg Locock


New here? Try reading these, they might help FAQ731-376
 
Upvote 0 Downvote
If the ground can be assumed to be infinitely stiff then the elevated portion of the beam can be viewed as being simply supported.[ ] If the lift-off at the end is small relative to the length of this simply supported beam then the simply supported beam can be treated as being very close to horizontal, and various small-angle simplifications will apply.[ ] The key deflection equation (using simple beam theory) is the one for the end rotation under a UDL:
[ ][ ][ ][ ][ ]wL³/(24EI)
Toss in F=wL/2, manipulate trivially, and you get:
[ ][ ][ ][ ][ ]h = 2F^4/(3w^3.EI)
 
Upvote 0 Downvote
Status
Not open for further replies.

Similar threads

AaronMcD
  • Question
Wood beam, long main span very short end span
Replies
2
Views
403
XR250
XR250
jreit
  • Question
Beam End Weld Design
Replies
2
Views
93
lexpatrie
lexpatrie
oengineer
  • Locked
  • Question
Design of CMU Bond Beam for One-Story Building
Replies
2
Views
62
phamENG
phamENG
JLC123
  • Question
Lifting Beam Design to BS13155:2020
Replies
3
Views
88
JLC123
JLC123
Dan.M.M
  • Locked
  • Question
LIFT DESIGN
Replies
9
Views
118
jayrod12
jayrod12

Part and Inventory Search

Sponsor

Back
Top