ShadowWarrior
Civil/Environmental
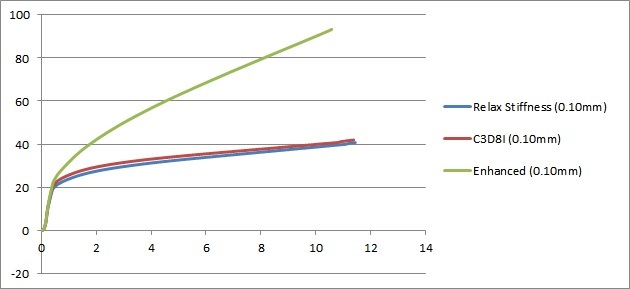
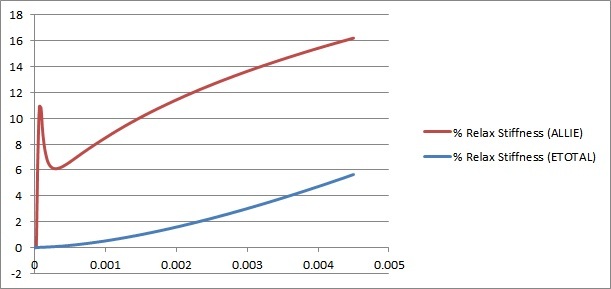
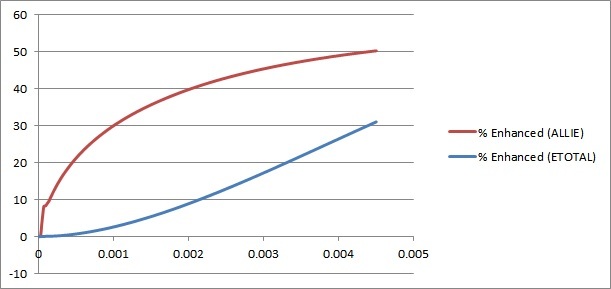
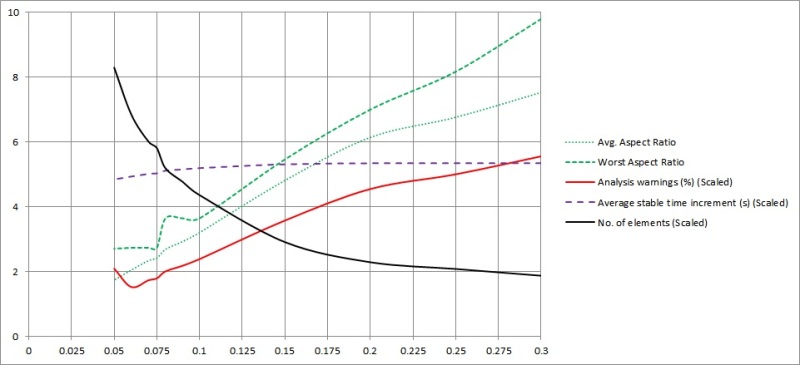
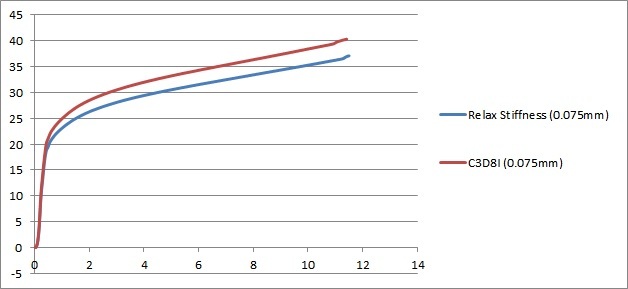
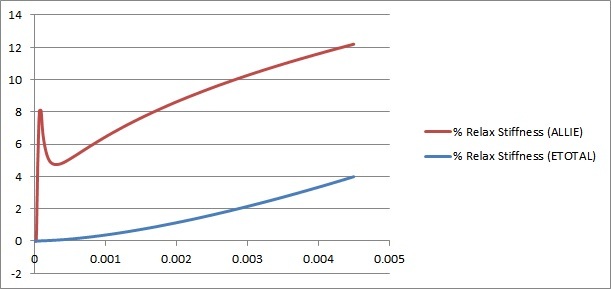
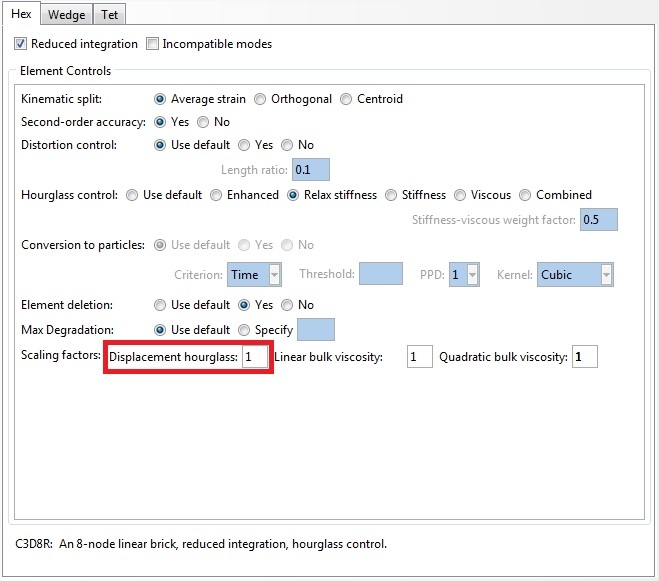
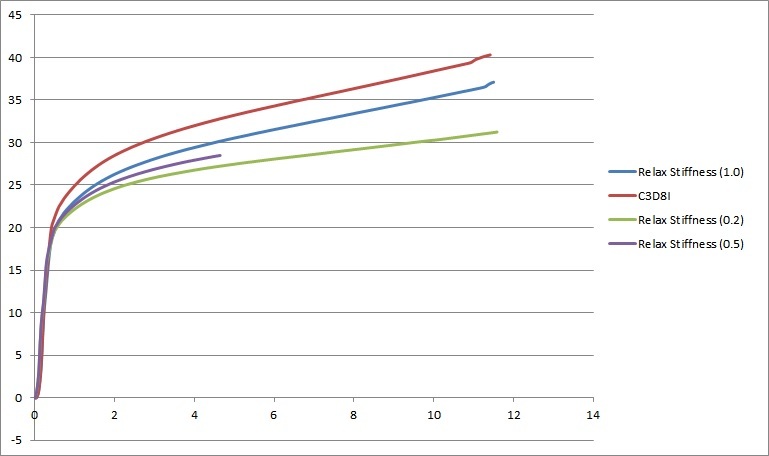
What is the guideline on Hourglass control energy limit?
Somewhere its suggested to keep it less than 1-2% of the Internal energy; somewhere else its less than 5% of Strain energy and somewhere else its said to be less than 10% of Total energy.
We need a definite guideline on this, a fixed parameter and a fixed value.
Somewhere its suggested to keep it less than 1-2% of the Internal energy; somewhere else its less than 5% of Strain energy and somewhere else its said to be less than 10% of Total energy.
We need a definite guideline on this, a fixed parameter and a fixed value.