Allowable concrete tensile stress across unreinforced plane?

[bugbus]

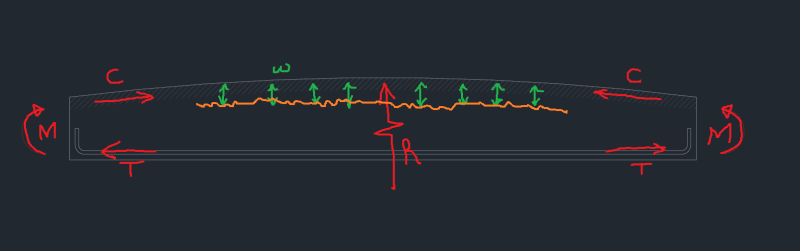
Consider the beam below which has a vertical curve in its top surface. The compression zone follows the shape of the top of surface and therefore generates tension through the depth of the beam (as indicated by the green arrows). For practical cases, this tensile stress would likely be very small (in the order of ~0.1 MPa or ~10 psi).

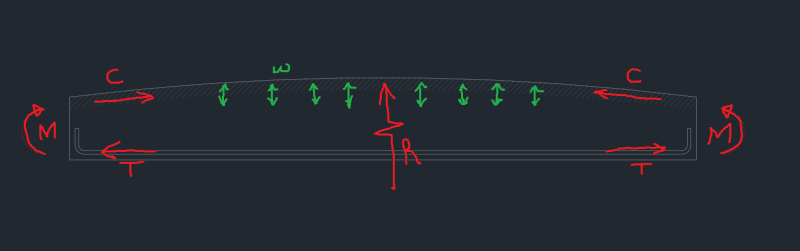
Obviously in this situation, we would most likely have vertical shear reinforcement which would resolve this splitting effect.

However, in theory, would it be acceptable to rely on the tensile strength of the concrete alone to resist this splitting effect? And if so, what would the allowable stress be?




As a PS, I just want to pre-empt people jumping in to say that concrete tensile stress should never be relied on for the strength of a structure (which I believe is simply not true). I can think of at least a few examples where this happens:

*The strength of bottle-shaped struts in strut-and-tie type problems in which the inherent tensile strength of the concrete can be relied on to prevent a splitting type failure (provided the stress induced by the splitting action is less than a certain limit, in the Australian codes this works out to be 50% of the characteristic direct tensile strength).
*Cast-in or post-installed anchors that may not necessarily rely on supplementary reinforcement and are held in place merely by the tensile strength of the potential failure cone.
*Development and lapping of reinforcement relies on the fact that concrete has an inherent tensile strength and therefore does not immediately split apart when the bars are loaded. I realise that in practical cases, the other reinforcement in the structure (fitments, etc.) can be relied on to provide this splitting resistance, but this is not always present.

 

[Lomarandil]

I would certainly allow stresses up to the modulus of rupture, and something in the back of my mind indicates that can be exceeded, but I can't recall the details at the moment.

 

[IDS]

Why would the tensile stress be so low?

In general the concrete will be cracked at the reinforcement level, and the cracks extend up to close to the neutral axis. For elements where there is no shear reinforcement the shear is carried through a strut and tie mechanism, with the reinforcement carrying the tensile force.

In practice some elements will have uncracked concrete, but they are not designed on that basis because if the concrete did crack it would fail suddenly and without warning.


Doug Jenkins
Interactive Design Services

http://newtonexcelbach.wordpress.com/

 

[Tomfh]

We rely on tension all the time. Rebar anchorage, shear transfer, etc. We put in so called “shear reinforcement” when the tension is too much, so as to intercept the cracks. If the tensile capacity of the concrete vanished our structures would collapse.

 

[bugbus]

@Lomarandil, to me that is probably too high of a limit where there is the risk of collapse. I think this would require a strength reduction factor in the order of 0.6 (in line with plain concrete requirements), along with a long-term tensile strength reduction factor of maybe ~0.5, and also using the characteristic direct tensile strength (which is less than the modulus of rupture).

This would give something in the order of 0.6*0.5*0.36sqrt(f'c) ~ 0.1sqrt(f'c), so maybe around ~0.5 MPa or ~75 psi for normal strength concrete.

 

[bugbus]

@IDS, I calculate (could be wrong, this was very quick) that the distributed load 'w' is equal to C/R, C being the compression force in the concrete, R being the radius of curvature for the top of the beam.

E.g. 600 (D) x 400 (W) beam, at 1% reinforcement and 500 MPa strength -> C ~ 1100 kN.

If R = 20 m, then the tensile stress across a horizontal plane would be (1100/20)/0.4 = 137.5 kPa.

 

[IDS]

gusmurr - If the steel force = -concrete compression = 1100 kN, then the bending moment = about 550 kNm and if the section was uncracked the maximum concrete tension would be about 23 MPa (M/Z = 0.55/0.024 = 22.9 MPa)

Doug Jenkins
Interactive Design Services

http://newtonexcelbach.wordpress.com/

 

[bugbus]

IDS, I was referring to the stress in the vertical direction caused by the curvature of the compression strut (tending to form a horizontal crack as shown in orange):

 

[IDS]

oops - I should have realised you weren't asking what I assumed you were. I probably should have looked at the sketch in the OP as well.

In that case your post at 03:51 seems reasonable.


Doug Jenkins
Interactive Design Services

http://newtonexcelbach.wordpress.com/

 

[Tomfh]

Gusmurr,

Why not apply the bottle strut rules?

 

[cooperDBM]

Are you accounting for any weight, including some self-weight, bearing on the top of the beam as a clamping stress?

 

[bugbus]

@IDS, all good thanks for your input

@cooperDBM, that's a great point and I'm sure it would basically solve the issue in a lot of situations

@Tomfh, I'm trying to think of any reason why the bottle strut rules couldn't be extended to other situations. There are only two things I can think of:

1) permanence of the loading - I feel that there ought to be some kind of long-term strength reduction factor for concrete subjected to sustained tension, especially if the dead load is a large proportion. Possibly this is already covered by the 0.5 factor in the code? It's not exactly clear why that factor is used;

2) size effect - looking at the Australian code for cast-in or post-installed anchors (similar to Appendix D(?) in ACI 318), the strength of the anchor is proportional to h[sup]1.5[/sup], so the anchors become proportionally weaker as the potential failure surface gets larger. Back-calculating the allowable tensile stress from the anchor code, it ranges from about 0.03sqrt(f'c) for large anchors (with potential failure surfaces having areas in the order of a few m[sup]2[/sup]), up to around 0.08sqrt(f'c) for quite small anchors. This is a little more conservative than the 0.1sqrt(f'c) that I proposed in an ealier post, but I hadn't considered the size effect previously. However, my understanding is that for anchors, not all the concrete failure surface can be utilised at one time, as the crack begins near the distal end of the anchor and propagates outwards along the cone-shaped surface (and this is probably the basis for the size effect). In the example I posted, the curved beam would experience more-or-less constant tension along its length and would tend to fail by splitting at one instant. Hence, possibly there would be less of a size effect and it might justify using a larger allowable tensile stress.

For bottle-shaped struts, the Australian code allows up to 0.18sqrt(f'c) tensile stress in the concrete, and there is no mention of a size effect. But similar to what I mentioned above, this may not be subject to the same sort of size effect as cast-in or post-installed anchors.


Anyway, enough rambling from me, I think I would be comfortable adopting an allowable tensile stress in the order of 0.1sqrt(f'c) [f'c in MPa] or 1.2sqrt(f'c) [f'c in psi].