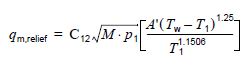An exchanger blocked in on the cold side contain vapor with flow in the hot side 5

[Hasab]

Hello my friends ,

I am dealing with over-pressure scenario where a PSV is set for exchanger blocked in on the cold side (the cold side contain only vapor fluid) with flow in the hot side, as i know there is an explanation for this scenario in API 521 where the fluid in the cold side is liquid not vapor (Hydraulic Expansion), which the suggestion there is a nominal diameter of (DN) 20 × DN 25 (NPS 3/4 × NPS 1) relief valve is commonly used. but if the fluid in the cold side is gas instead of liquid, is there any rule or equation explain how to determine the required flow rate through the PSV in this instance?
( As per my understanding, the over-pressure in this case will result form the expansion of the trapped gas (might be in the tube or the shell) heated up by the hot side fluid, i did not find any standard or equation can be used to determine the required flow rate for this contingency).
could someone have idea give any help or suggestion. thanks to everyone in advance.

 

[TiCl4]

First you need to confirm that the vapor in question will actually overpressurize the cold side when heated. If this is indeed an over-pressure case, my initial thought is to look at it as a constant pressure expansion due to heat input. When your PSV initially lifts, your pressure in the heat exchanger will remain constant and the gas will begin to expand through the PSV at constant source pressure. This initial expansion flow is your flow case. This is assuming that the lifting quickly relieves the necessary moles of vapor to drop pressure below valve reseat pressure, and that pressure does not rise above PSV set pressure.

You can check those assumptions by looking at the duration of flow. I have not sized a PSV for this type of case before, but I find it hard to imagine the PSV would be very large unless your cold side volume is very large.

Perhaps others with direct experience could provide more insight.

 

[don1980]

This case requires that you identify the starting conditions (T&P of the low pressure side) and then the next step is revealed by thinking through the dynamics of what actually occurs after the cold side is isolated. The cold vapor temperature starts to rise, resulting in the pressure rising. You can use PV/T = PV/T to determine the temperature at which the pressure reaches the PSV set pressure. After burping out some hot vapor, the PSV re-closes. Then the same process starts again, but this time the starting T is the final T in the first iteration. After a few of these cycles the cold side T will reach the hot side T, after which the the scenario is over with - obviously no more pressure rise.

The required relief rate is the rate at which the vapor expands, after the pressure has risen to the set pressure. An accurate determination of the required relief flow depends entirely on the rate at which the temperature rises. This is hard to accurately determine, and it's a dynamic situation - the rate of temperature rise continuously decreases as the cold side T gets hotter. Since the required relief flow is going to be small, there's little incentive to try to do rigorous calculations to plot the rate of temperature rise. In most cases, even a ridiculously conservative rate of temperature rise will still result in a small PSV. The rate of heat transfer inside the exchanger is going to be poor since there's no flow on the cold side. That is, the film coefficient is going to be very low. Using the design value for overall U coefficient would be extremely conservative, but that value is easy to obtain and it's acceptable for this calculation (there's very little penalty for being grossly conservative). Alternatively, you may find that the size of the PSV is small even based on estimating an extremely high rate of temperature rise. I think that's OK too.

 

[Hasab]

Thank you TiCl4 (Chemical).
As you said, we first need to check whether the pressure rise due the expansion is able to cause overpressure or not. in some situation the rise in the pressure will still under the design pressure of the equipment. we can use the relation P1V1/T1 = P2V2/T2 to verify this point by sitting the final temperature T2 equal to the hot side fluid max. temperature and get the corresponding pressure P2.

 

[Hasab]

Thank you don1980 (Chemical).
As i have understood, by using the heat duty of the exchanger as rate of heat transfer as a conservative approach for temperature rising, and with knowing the value of the thermal expansion coefficient of the vapor, we can then determine the expansion rate of the vapor (which is the required relieving rate).
the heat duty is calculated by:
Q = M * Cp * ∆T
Where;
Q – is the heat duty or the total heat transferred. Btu/hr or W

M – is the Mass flow rate for the fluid undergoing the temperature change. lb/hr or kg/s

Cp – is the heat capacity of the fluid undergoing the temperature change. Btu/lb.°F or J/kg.°K


is this correct? ( may any one advice if any )

 

[PaoloPemi]

in my opinion, in order to verify if a PSV is required, since there is flow in the hot side you do not need to solve heat balance but could presume that, within a reasonable time interval
t (mix) cold side | ~ | (some average value) t hot side
you can calculate the final pressure for a given volume (the fluid blocked in cold side) and temperature (some average final value as result of heat transfer with fluid in hot side),
this is a standard Volume-Temperature flash operation available in thermodynamic libraries as for example Prode Properties, or process simulators etc.
as alternative you can estimate the final pressure with ideal gas law , for example P2 = P1 * T2 / T1
Once you have established that a PSV is required, in order to estimate the (max, design) flowrate you need to solve a series of mass & heat balances,
normally I solve these problems with Python or Excel and the called direct integration method,
basically, you calculate in sequence a certain number of conditions (T,P,flows) and the procedure is equivalent to dynamic simulation in process simulators,
also in this case you can adopt simplified models (ideal gas law, constant cp etc.) for preliminary estimates.

 

[Hasab]

Thank you PaoloPemi (Mechanical). i got your point.
Yes i used the relation P2 = P1 * T2 / T1 to determine the final pressure. the volume of the vapor trapped between the blocked valves is fixed, and also its amount.

 

[MortenA]

Hasab, dont know how familiar you with the ideal gas law - its not accurate at higher pressure and temperature and the temperature is absolute (Rankin or Kelvin) and the pressure is absolute (not gauge). Say that you cold side is 20ºC and your hot 50º, this works out at 293K and 323K and the pressure increase is thus 10% (not 250% if you used ºC)

Best regards, Morten

 

[georgeverghese]

In API 520 ( sizing of RVs'), there is a procedure for gas phase (blocked in) thermal expansion due to fire. In this procedure, Tw is usually taken to be 1100degF during fire. in your case, set Tw to be the max hot side temp to get the required RV orifice size. And the exposed surface area would be the total tube side surface area.

 

[Hasab]

@ georgeverghese (Chemical), in this procedure when i set Tw to be max. hot side temperature, its value came lesser than T1 (the relieving temperature), this way the equation can not be used (it will result in negative base for the exponent 1.25). The equation is in API 521

T1 is the relieving temperature, calculated by the equation

P1 is the relieving pressure.

I think this means the hot side temperature is not high enough to cause the cold side vapor to expand to the degree which can result in over pressure scenario, in this time the differences between cold side operating temperature Tn (the temperature at the time of the blocked in) and the hot side max. temperature is small.

 

[georgeverghese]

Okay, so you dont have a thermal ( non fire) blocked in relief case.

 

[Hasab]

@ MortenA (Petroleum), Yes the law is not accurate at high pressure values & low temperature values because of the effect of gas inter-molecular forces in these conditions.
I am using the law in 35 C & 7.3 bar(a) initial conditions for the gas, i will verify the applicability of the law for this situation. however i would like if anyone have an idea about when the ideal gas law doesn't work accurately, i mean are there any specific values for the pressure & temperature above or under which the law will not give reliable values, or it is a relative matter need to verified for each particular case individually ( i.e. might the pressure value in one certain case do not considered high while this same value seen as high in another situation).

 

[PaoloPemi]

Hasab,
what do you mean about accuracy of ideal gas law ?
with the mentioned formulation
P2 = P1 * T2 / T1
you solve P1*V1=Z1*R*T1 , P2*V2=Z2*R*T2
assuming V2 = V1 and Z2 = Z1
however Z is not constant, for example Peng Robinson cubic EOS predicts a Zc about 0.3 near critical point,
as you see presuming a constant Z can originate large errors,
it can work for limited ranges (i.e. P2~P1 , T2~T1)

 

[MortenA]

@paolopemi, once you add the "Z" its not the Ideal gas law (obviously). So if you dont have a tool to determine Z its not much help.

 

[PaoloPemi]

the formulation P2 = P1 * T2 / T1 includes the contribute of Z but as constant value Z(P1,T1),
consider the case of C1 at 210 K 50 Bar.a , Z = 0.659 (GERG 2008) , V = 0.0143... m3/Kg
if you solve a V-T flash operation with V = 0.0143... m3/Kg , T = 220 K the result is 54.99..Bar.a
at 220K, 54.99 Bar.a Z = 0.692
now if you solve with the simplified correlation
P2 = 50 * 220 / 210 you get 52.4... Bar.a
however if you add the correction for Z2 / Z1 due to the fact that Z is not constant over this range
P2 = (0.692/0.659) * 50 * 220 / 210 ~ 55 Bar
which confirms what said in my previous post

 

[Hasab]

@ georgeverghese (Chemical), yes i think the scenario will not happen

 

[Hasab]

@ PaoloPemi (Mechanical), thank you for the new information. suppose there is the initial condition T1=20C & P1=8barg, my query is just by looking on the initial values can we decide whether the ideal gas law can be used or not, i.e. can we use P1/T1=P2/T2 to calculate one of the final values P2 or T2?
also another thing, is the relation P1/Z1T1=P2/Z2T2 correct and can be used( may anyone advice)

 

[PaoloPemi]

short answer : for accuracy prefer a EOS,
see the example provided in my post 9 Jun 20 09:41
you can calculate / estimate Z1 and Z2 to correct P2 = P1 * T2 / T1
of course, when Z2 is not too different from Z1 (low pressures, conditions far from critical area) errors can be limited,
if you know the composition, you can solve a Volume-Temperature flash operation (with a simulator or a thermodynamic library as discussed).

 

[Hasab]

@ PaoloPemi (Mechanical), thanks clear. EOS is good option for me.

 

[MortenA]

Paulopemi, dont get me wrong i agree with your estimate!