deltak2
Structural
- May 14, 2022
- 2
Hi everyone,
Some questions for you guys on the buckling evaluation of a doubly-curved shell using ASME Code Case N-284-4.
1. According to -1712.1.4, “toroidal and ellipsoidal shells shall be analyzed as equivalent spheres” to calculate their theoretical buckling stress.
1.1. How shall we determine the radius of the equivalent sphere? I find no instructions in the code case.
1.2. We know buckling would not occur for a sphere under internal pressure, as no compressive or shear stress is induced in this case. Does this imply that the “equivalent sphere” method is only applicable to the case under external pressure?
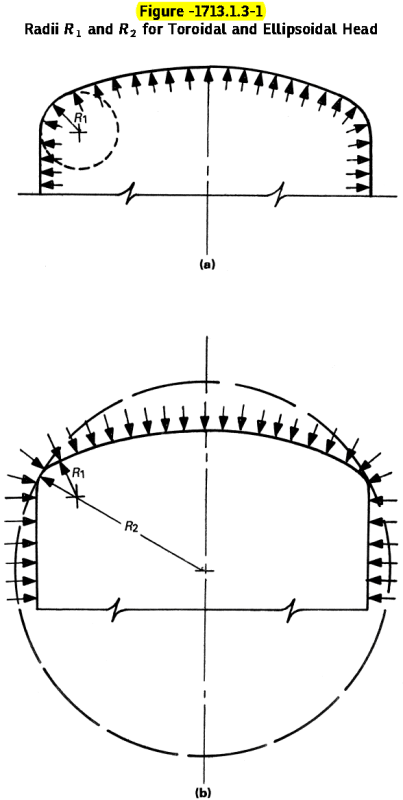
3. According to -1713.1.3, the calculation of allowable stresses of a toroidal or ellipsoidal shell for the special stress states of uniaxial compression and equal biaxial compression involves the determination of the effective stress radii, R1 and R2, and a figure is given for R1 and R2 (see below).
3.1. How shall we determine R1 and R2? I find no instructions either in the code case.
3.2. Do R1 and R2 have something to do with the radius of the equivalent sphere mentioned above?
Any comments and advice are highly appreciated.
Some questions for you guys on the buckling evaluation of a doubly-curved shell using ASME Code Case N-284-4.
1. According to -1712.1.4, “toroidal and ellipsoidal shells shall be analyzed as equivalent spheres” to calculate their theoretical buckling stress.
1.1. How shall we determine the radius of the equivalent sphere? I find no instructions in the code case.
1.2. We know buckling would not occur for a sphere under internal pressure, as no compressive or shear stress is induced in this case. Does this imply that the “equivalent sphere” method is only applicable to the case under external pressure?
3. According to -1713.1.3, the calculation of allowable stresses of a toroidal or ellipsoidal shell for the special stress states of uniaxial compression and equal biaxial compression involves the determination of the effective stress radii, R1 and R2, and a figure is given for R1 and R2 (see below).
3.1. How shall we determine R1 and R2? I find no instructions either in the code case.
3.2. Do R1 and R2 have something to do with the radius of the equivalent sphere mentioned above?
Any comments and advice are highly appreciated.

