Beam deflection problem with multiple Uniformly Distributed Loads

[everydayengineer]

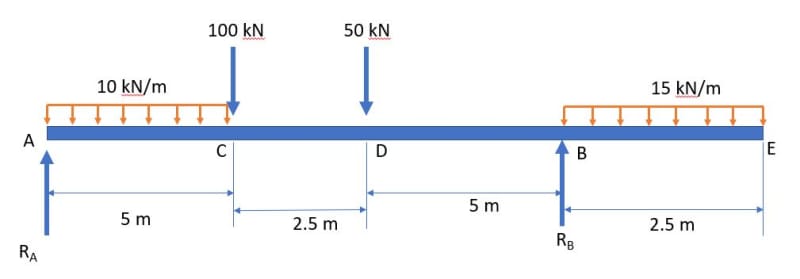
Hi all,

I am trying to solve this beam problem to find the deflection at different points along the length of the beam. However I am having a hard time writing the equation for bending moment using Macaulay's theorem since there are 2 uniformly distributed loads of different magnitudes.

Can someone help solve this problem?

Thank you in advance!

 

[BAretired]

Your structure is statically determinate, so you can solve for R[sub]A[/sub] and R[sub]B[/sub] directly. From there, you can find the moment at any point distant 'x' from Point A using simple statics.

Macaulay's Theorem is just another name for the Double Integration Method. I was going to refer you to the following for a simple example of a beam with a point load at midspan. Unfortunately, the man in the video gets the expression for dy/dx (slope) and y (deflection) wrong. Can you find his error?

https://www.youtube.com/watch?v=cSzzTbA267I

Personally, I would not use the Macaulay Theorem to solve this problem, unless you are required to use it in your assignment. There is nothing wrong with the method, but with that many loads, it is very easy to drop a term or make some arithmetic error. There are a number of easier ways to solve it. One method would be to treat each load separately, then use superposition to find the combined answer for slope and deflection at any point distant 'x' from Point A.

We can't solve your problem for you, but it really is pretty straightforward, even though it has a lot of terms. Start by solving for the two reactions, then express the moment at any point distant 'x' from Point A and show us what you've got.

BA

 

[GregLocock]

Yup superposition is the way to go.

Cheers

Greg Locock


New here? Try reading these, they might help FAQ731-376

http://eng-tips.com/market.cfm?

 

[1503-44]

There is not a one-equation continuous solution. There are four (4) equations needed. One of the 4 equations will be valid within each range between loading conditions.

 

[BAretired]

There is not a one-equation continuous solution. There are four (4) equations needed. One of the 4 equations will be valid within each range between loading conditions.

Correct, although there are similarities in the equations, some having additional terms accounting for different ranges. That point was missed by the instructor in the video which I mentioned earlier. He used the wrong expression when finding the slope at Point A and came up with the wrong answer. (see below)

Although he came up with the correct answer for deflection at midspan, his expression for deflection was not valid for the left half of the beam.

BA

 

[BAretired]

If boolean expressions are used, a single equation can be written for the whole span.

M[sub]x[/sub][sub][sub][/sub][/sub] = R[sub]A[/sub].x - P(x-a)(x>a) - Q(x-b)(x>b) - R(x-c)(x>c)​

is the moment at any point of a simple span beam, distant x from Point A, with point loads P, Q and R at a, b and c respectively from Point A. The boolean expressions, shown in red have the value of 1 or 0 depending on whether the bracketed expression is true or false.

BA

 

[everydayengineer]

I was confusing myself thinking I could write one nice complete moment equation that would tell me the deflection at any point. but that is wrong because the bending behavior differs at each section of the beam.

I was actually able to write moment equations for individual sections and integrated them twice(which ended up with a lot of constants of integration - 8 in total). Then I applied multiple boundary conditions to solve for all the constants. boundary conditions were:
1. deflection = 0 at supports - (solved for 3 constants).
2. deflection is the same at a particular point, meaning I could equate the deflections given by 2 different equations (points C and D) - (solved for 2 constants).
3. slope is the same at a particular point, meaning I could equate the slopes given by 2 different equations (points C, D and B) - (solved for 3 constants).

Thus I now have different bending moment, slope and deflection equations for different sections of the beams!

thank you all for the great inputs

 

[BAretired]

Happy to hear you found the solution. Congrats!

BA

 

[drawoh]

BAretired,

I was taught to write equations like that as...

M[sub]x[/sub] = R[sub]A[/sub]x - P<x-a> - Q<x-b> - R<x-c>,​

with the pointy brackets being zero if the contained value was equal to or less than.

--
JHG

 

[BAretired]

Okay, that is clear and easier to write. I have not run into that notation until now, but it makes sense.

BA

 

[Jacob Henry]

Great. you found your solution. happy to see this.