Astrostructural
Structural
- Mar 26, 2020
- 2
Hi everyone,
It might seem like too simple a Question for many but I would like to calculate the Von Mises stress for a beam in biaxial bending. The bending stresses run along the beam axis so they can be added up at the Cross section Corners, but I would like to find the maximum Von mises stress including the components of shear stress as well. There is also an axial load on the beam, that generates its own normal stress. I have attached a diagram for explanantion.
At which Point on the Body should the Von mises stress be calculated to obtain a maximum value?
My bending stresses are 303 MPa for Sigma bxk, and 408 MPa for Sigma bxs(Qz,) and maximum txz (Qz) is 16 MPa, and maximum txy is 132 MPa.
Thank you all in advance
Regards
Asutosh
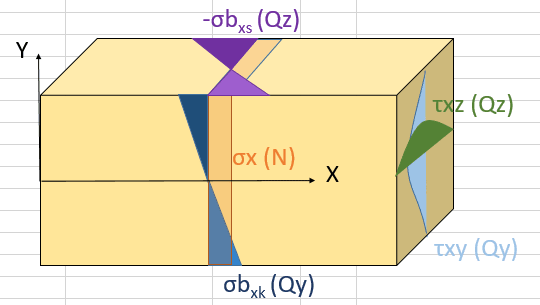
It might seem like too simple a Question for many but I would like to calculate the Von Mises stress for a beam in biaxial bending. The bending stresses run along the beam axis so they can be added up at the Cross section Corners, but I would like to find the maximum Von mises stress including the components of shear stress as well. There is also an axial load on the beam, that generates its own normal stress. I have attached a diagram for explanantion.
At which Point on the Body should the Von mises stress be calculated to obtain a maximum value?
My bending stresses are 303 MPa for Sigma bxk, and 408 MPa for Sigma bxs(Qz,) and maximum txz (Qz) is 16 MPa, and maximum txy is 132 MPa.
Thank you all in advance
Regards
Asutosh

