Buckling Load

[Mateus_R]

Dear all,

I have to evaluate the effect of the buckling in a bar, and some questions arise, specially regarding the ANSYS Mechanical interpretation:
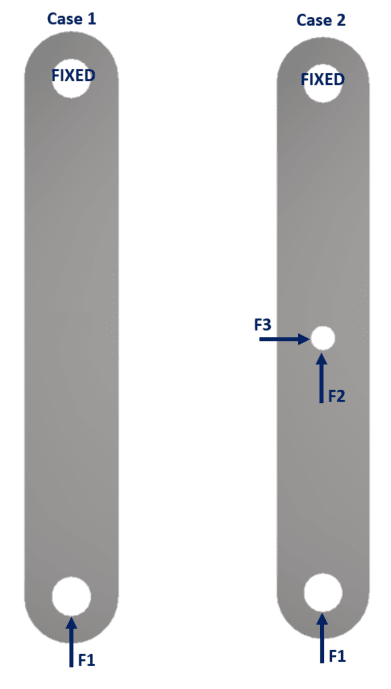
Suppose I evaluate buckling according to image attached, case 1 -> Ansys will give me the critical buckling load related to the applied load, by means of the loading factor, and this is straightforward.

Suppose case II - now I have two compression forces located at different points. Ansys still gives me the loading factor, but in this case how can I interpret it? How the loading factor is related to each of the two forces?

Thank you for your support.

 

[JAE]

You should repost this in forum569 as this is a question about the software, not structural engineering directly.

Check out Eng-Tips Forum's Policies here:
faq731-376

 

[ThomasH]

I don't use Ansys but my assumption is that it is the same as for case 1. Buckling load is the three forces multiplied by the load factor.

If you ask in the Ansys forum you may get more reliable information.

Thomas

 

[FEA way]

I remember that in ANSYS documentation there is a description of procedure necessary in case of more than one compressive load. Critical load factor is used to scale all loads existing in the model. If one load is constant (dead load) a way to solve this is to iterate changing another (variable) force until the load factor becomes approximately 1.

 

[Mateus_R]

Thank you for the warning. I will upload the question in the software forum.

Regarding the structural analysis for case 2, if I'd like to confirm the values with some hand calculation, do you suggest to use superposition of effects from both forces, considering that one force works in the whole length and the other just at half length?

 

[ESPcomposites]

There are two types of buckling analysis:

1. Eigenvalue buckling. In this case, the predicted buckling load is the reported Eigenvalue multiplied by the applied load(s). This is probably what you are running (i.e. you are probably referring to the Eigenvalue when you say scaling factor). The approach will be the same for both cases you presented. Some also call this "linear buckling" because all the loads are scaled.

2. Nonlinear buckling. This case is quite different and you would apply the actual load and determine the response (along with a geometric nonlinear analysis and a perturbation, if required). There is no scale factor or Eigenvalue.

For the second case in your picture, you have what is called a "beam-column" since F3 causes beam bending (unless the magnitude is very small). This is a nonlinear phenomenon and there is a -coupling- between the axial compression load and the beam bending. F3 tends to destabilize the column and the critical F1 load will be a function of F3.

Brian

http://www.structuralfea.com

 

[BAretired]

I would suggest solving the problem by hand using Newmark's Numerical Procedure.

BA

 

[BAretired]

Regarding the structural analysis for case 2, if I'd like to confirm the values with some hand calculation, do you suggest to use superposition of effects from both forces, considering that one force works in the whole length and the other just at half length?

This is a case where superposition does not yield the correct answer. The superposition principle, also known as superposition property, states that, for all linear systems, the net response caused by two or more stimuli is the sum of the responses that would have been caused by each stimulus individually. In Case 2, moments and deformations for each force are or may be affected by each of the other forces acting simultaneously.

To determine a buckling load for three forces acting simultaneously, more information is required. One could assume that F2/F1 = c and F3/F1 = k where c and k are constants. From the start of loading to the buckled state, those ratios would need to be maintained. Otherwise, the solution has an infinity of correct answers.

BA