Calculating Moments of a Tank Wall of Water

[MatthewMansfield]

Hello all,

I was hoping someone could help me calculate the moment a tank wall experiences.

I have the following question:-

Tank contains water with dimensions:
4m Wide
12m Long
3m Tall

Determine the moment at the bottom of the long side at its centre.

I have drawn a sketch of the tank and highlighted in dark what I believe is the "bottom of the long side"

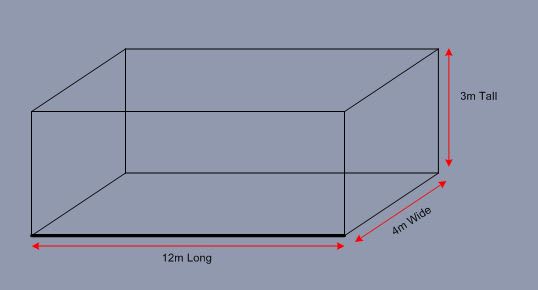
To calculate the force acting on the wall (12 x 3) I have done the following:-

F = p * g * a * y
p = density of water (1000)
g = gravity (9.81)
a = area (36)
y = distance from the top of the tank to the walls centroid (1.5)


1000 * 9.81 * 36 * 1.5 = 529740 N of force acting on the wall.

I am not really sure where to go from here?

Can anyone help?

 

[JAE]

Here's a few links:

http://ceae.colorado.edu/~silverst/cven4830/Rectangular_Tank_Example_Latest.pdf

http://members.cement.org/EBiz55/ProductCatalog/Product.aspx?ID=2104

https://www.amazon.com/Pca-Rectangu...gular+Concrete+Tank+Design+Manual&rh=n:283155

 

[fel3]

And another one:

https://www.usbr.gov/tsc/techreferences/hydraulics_lab/pubs/EM/EM27.pdf

This subject is also covered in "Roark's Formulas for Stress and Strain" (it's in Chapter 11 in the 8th edition). The current (6th) edition of Roark's is available through Amazon. PDFs of older editions can be found on-line.

============
"Is it the only lesson of history that mankind is unteachable?"
--Winston S. Churchill

 

[jdonville]

There are moments acting in at least two orthoganal directions: The first acts around an axis parallel to your "long side". The second acts around the vertical axis of the "long side" wall.

I will simply use the term "gamma" to denote the unit weight of water to attempt to keep things simpler.

Force due to water pressure on each of the walls is equal to 1/2 x gamma x (depth^2) per unit length of wall. As the pressure distribution is triangular (linearly increasing from the top of the vessel), the resultant force acts at a distance of depth/3 from the bottom of each wall. The pressure on the bottom of the vessel is constant at gamma x depth per unit area.

The problem is complicated a bit by the fact that the short side walls and bottom of the vessel act as restraints against displacement (and rotation about the edges) of the "long wall" at and along the each of the common edges.