lomarandil said:
I am primarily thinking about this for the effect on shear capacity and maximum stirrup spacing.
Meeeee too! I've been thinking about this on and off for years now. I doubt that I actually have the answer on this one but, at the least, perhaps I can stimulate some interesting discussion. Take everything that follows as being at least part conjecture.
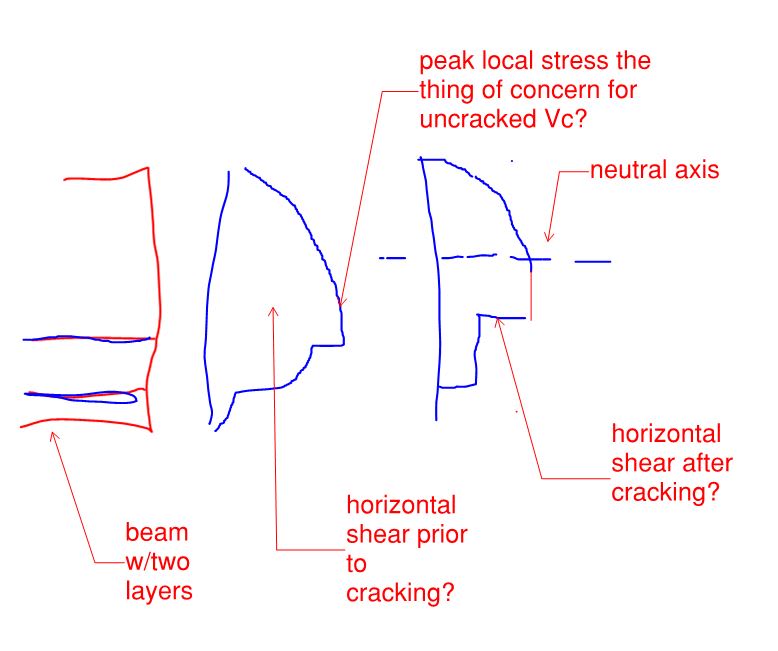
1) In what follows, consider the two sketches of horizontal shear below, across a beam both prior to cracking and after cracking. I've probably screwed up the exact shapes but, hopefully, I've captured the salient features.
2) Vc.... ohhhh Vc. My understanding of Vc is this:
a) Prior to shear cracking cracking, you're trying to prevent the peak, local shear stress from exceeding the value that would initiate cracking. Check.
b) After shear cracking, we assume that the cracked Vc is the SAME as the
uncracked Vc. Frankly, I've long been astonished at this. Hopefully I'm either wrong about it or it's been validated through some testing that I don't now about.
3) Based on #1 & #2, it seems rational to me that, for the purpose of calculating Vc_uncracked, which becomes Vc_cracked:
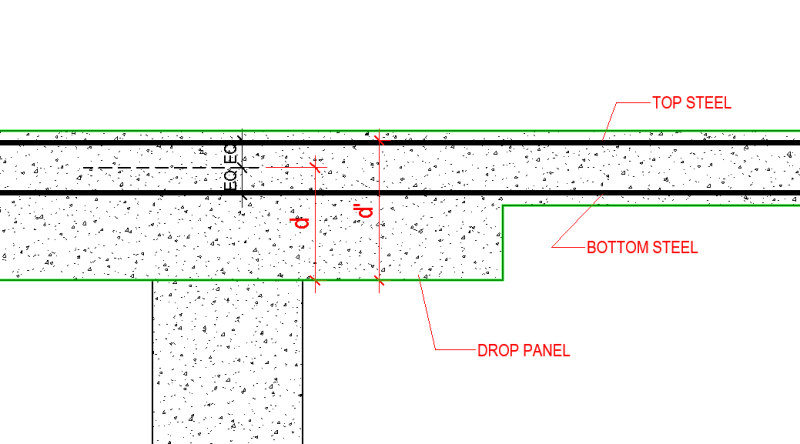
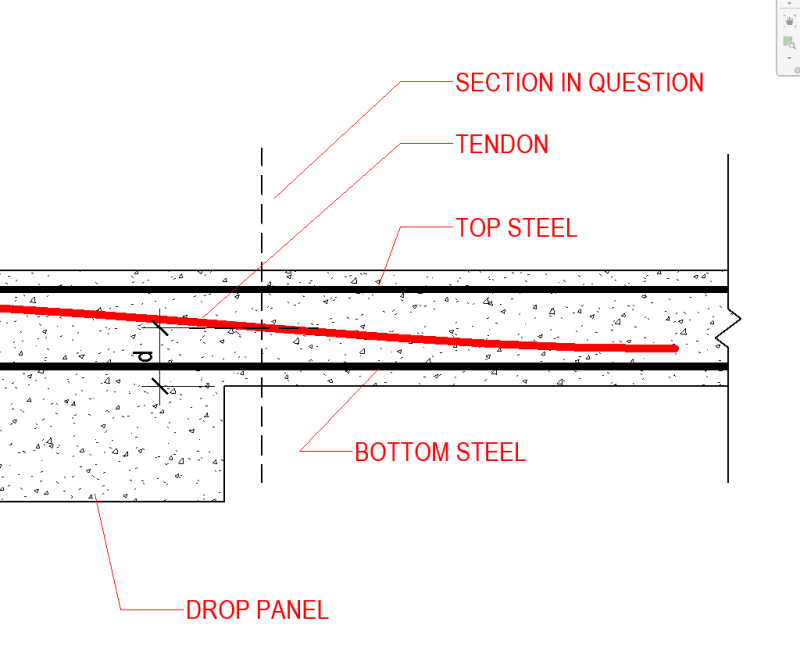
a) The most
accurate estimate of the shear depth would be to the centroid of the tension force, including all reinforcement by way of strain compatibility.
b) The most
conservative estimate of the shear depth would be to the centroid of the tension reinforcement since this increases your averaged shear stress (Vu/bd). Of course, this reopens the question of whether or not one should include rebar not intended to be flexurally active.
In both cases, I feel that you're looking for an averaged value (Vu/b*dv) that captures the peak shear stress value for the cross section prior to shear cracking.
4) My understanding of the minimum stirrup spacing is that the goal is to have a minimum number of stirrups cross each potential shear crack. This almost suggests that one could use the depth to the extreme tension steel for this purpose. That said, if our shear design methodology is based on the truss model, then each assumed concrete diagonal needs to touch down where there is sufficient flexural tensile capacity to restrain it longitudinally. And the lowest layer of steel cannot, by definition, supply that by itself. So, for stirrup spacing, I feel that the center of tension is again the most theoretically correct answer. All of this is muddied by the fact that your location of peak moment is not simultaneously your location of peak shear. At the end of a simple span beam, I think that one could argue that the shear depth, for the purpose of stirrup spacing, could be based on the flexural steel actually
required at that location, not the flexural steel
supplied at that location.
5) At the end of the day, we might just have to accept that shear design is rough stuff, particularly the conventional, non-compression fielded theory formulations of shear design. A truly precise definition of the shear depth based on theory is elusive.