Hello, I have some questions regarding clamping force.
I have a two-piece cylindrical clamp which is to be clamped around a cylindrical part. It is a clamp installed on a product during transportation, where lashings go between the clamp and trailer.
The coefficient of friction and surface area between clamp and cylinder is known.
How would I go about finding the necessary clamping force to ensure the clamp does not slide down the cylinder, nor rotates around its own axis? There is to be a tension force applied in the two brackets.
I applied the forces which I believe will have an affect on the clamping force, but I believe the tension force will make the clamping force non-uniformly distributed across the cylinder.
From what I have found so far, the hoop stress may be relevant. I also looked at Roark's Formulas For Stress And Strain, it had a chapter (9.3) about circular rings and arches, this may also be relevant.
This is completely new to me, and I struggle to find good literature about the topic, so any help is greatly appreciated!
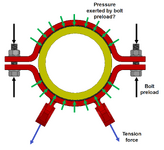
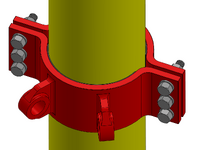
I have a two-piece cylindrical clamp which is to be clamped around a cylindrical part. It is a clamp installed on a product during transportation, where lashings go between the clamp and trailer.
The coefficient of friction and surface area between clamp and cylinder is known.
How would I go about finding the necessary clamping force to ensure the clamp does not slide down the cylinder, nor rotates around its own axis? There is to be a tension force applied in the two brackets.
I applied the forces which I believe will have an affect on the clamping force, but I believe the tension force will make the clamping force non-uniformly distributed across the cylinder.
From what I have found so far, the hoop stress may be relevant. I also looked at Roark's Formulas For Stress And Strain, it had a chapter (9.3) about circular rings and arches, this may also be relevant.
This is completely new to me, and I struggle to find good literature about the topic, so any help is greatly appreciated!


