-
1
- #1
Columb
Mechanical
- Sep 18, 2008
- 7
Hello
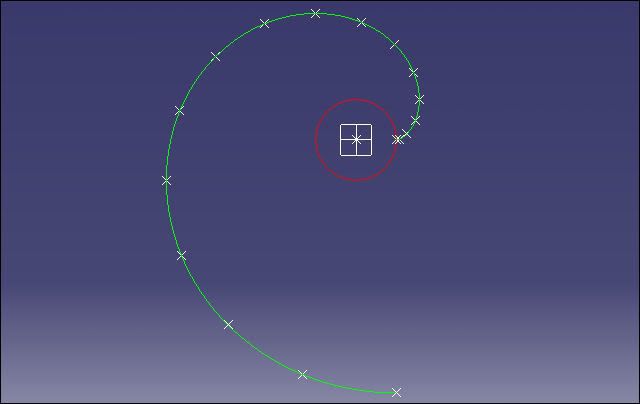
How should I create a curve by equation?
The equation is the involute equation:
x=r(cos(t)+t*sin(t))
y=r(sin(t)-t*cos(t))
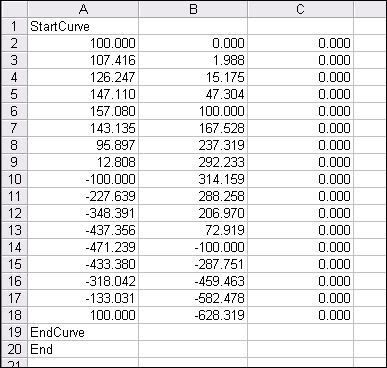
r and t are known and I can get the points(x,y)but I need to draw the curve.
Thanks
Columb
Columb
How should I create a curve by equation?
The equation is the involute equation:
x=r(cos(t)+t*sin(t))
y=r(sin(t)-t*cos(t))
r and t are known and I can get the points(x,y)but I need to draw the curve.
Thanks
Columb
Columb