Baffled Engineer
Structural
- Jul 27, 2018
- 57
What is the correct limitation on slenderness of legs of angles for a double angle compression chord of a girder truss?
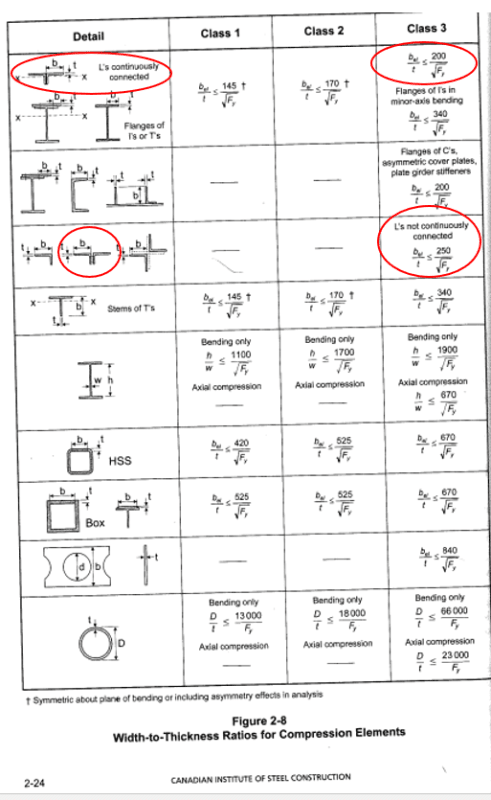
I have attached the relevant tables below.
The angles are primarily resisting compressive forces but there are some minor flexural stresses as well.
My confusion stems from the fact that under pure axial compression, table 1 allows a slenderness of 250/sqrt(Fy), but under flexural compression, Table 2 allows for a more stringent slenderness limit of 200/sqrt(Fy). Intuitively, I would think an angle leg under full compression is more critical than a leg under flexural compression so it doesn't make sense why the slenderness is more critical under flexural compression.
The existing angles that I'm working on are 2L6x4x1/2 LLBB and 2L7x4x1/2 SLBB with an Fy of 300mPa, and the slenderness I have are between 200/sqrt(Fy) and 250/sqrt(Fy)... which would make them class 4 if the correct slenderness limit is 200/sqrt(Fy).
I appreciate the help guys. Thanks.
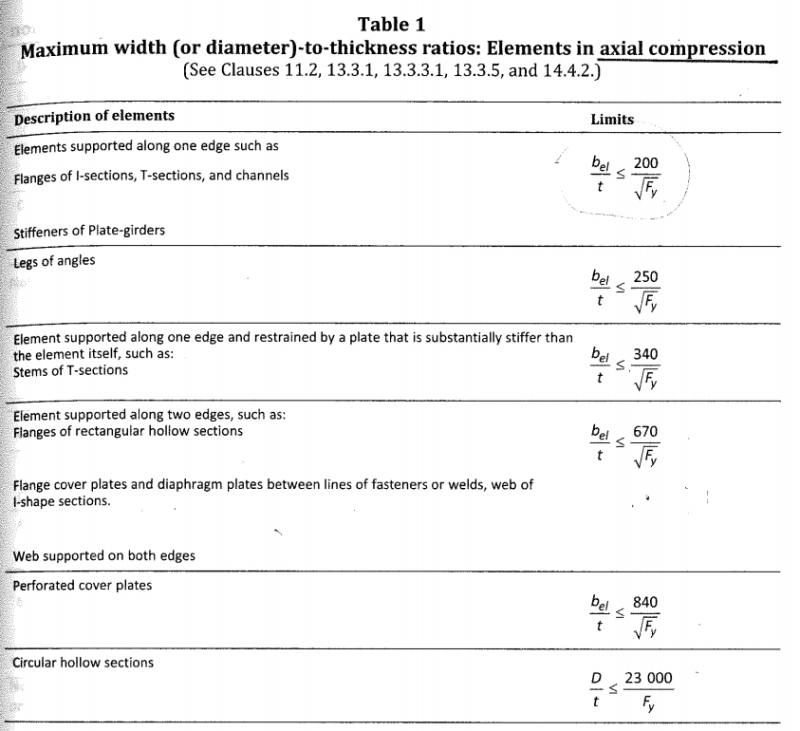

I have attached the relevant tables below.
The angles are primarily resisting compressive forces but there are some minor flexural stresses as well.
My confusion stems from the fact that under pure axial compression, table 1 allows a slenderness of 250/sqrt(Fy), but under flexural compression, Table 2 allows for a more stringent slenderness limit of 200/sqrt(Fy). Intuitively, I would think an angle leg under full compression is more critical than a leg under flexural compression so it doesn't make sense why the slenderness is more critical under flexural compression.
The existing angles that I'm working on are 2L6x4x1/2 LLBB and 2L7x4x1/2 SLBB with an Fy of 300mPa, and the slenderness I have are between 200/sqrt(Fy) and 250/sqrt(Fy)... which would make them class 4 if the correct slenderness limit is 200/sqrt(Fy).
I appreciate the help guys. Thanks.