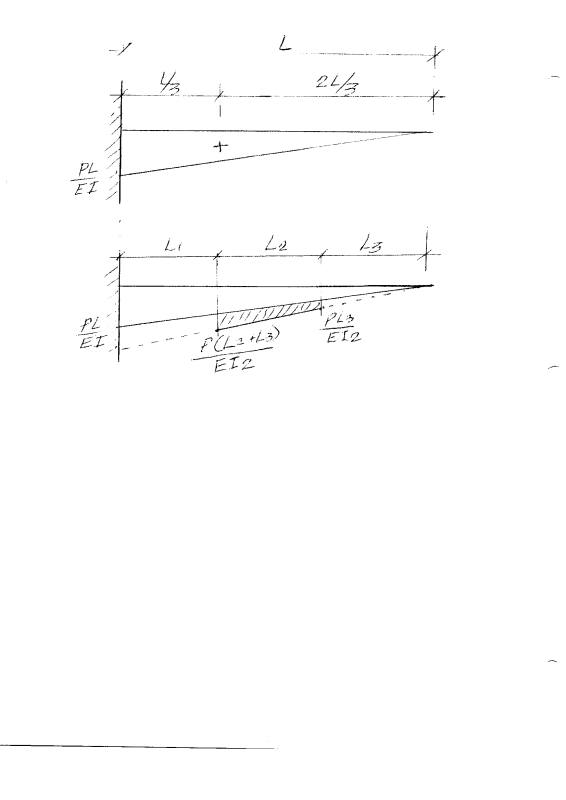
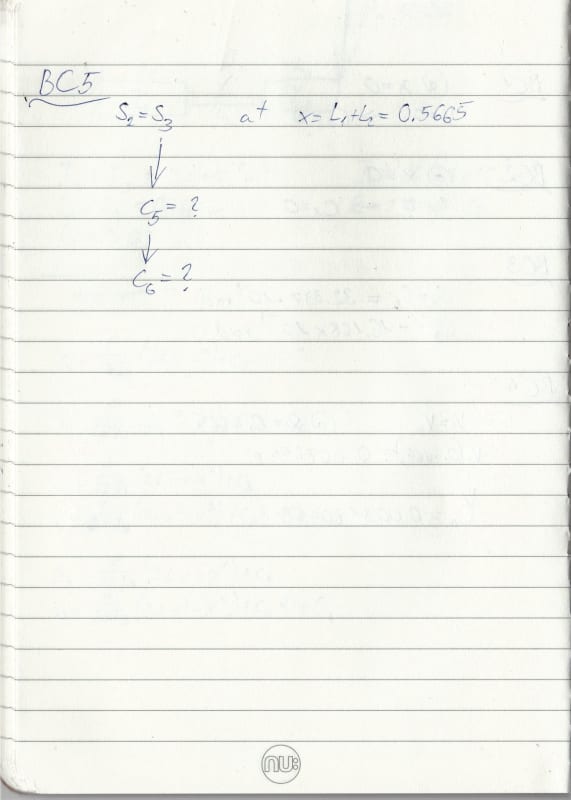Hello Everyone,
I am trying to calculate the maximum deflection of a beam that has a variable cross-section.
I have tried to follow this method:
However, my beam consists of 3 sections. Therefore, I extended the method shown in the article.
I can't seem to get right the last equation for this problem.
I have plotted my first two equations in MATLAB and they seem to give sensible results (aligned with FEA results).
Can someone check if I am using the right approach, please?

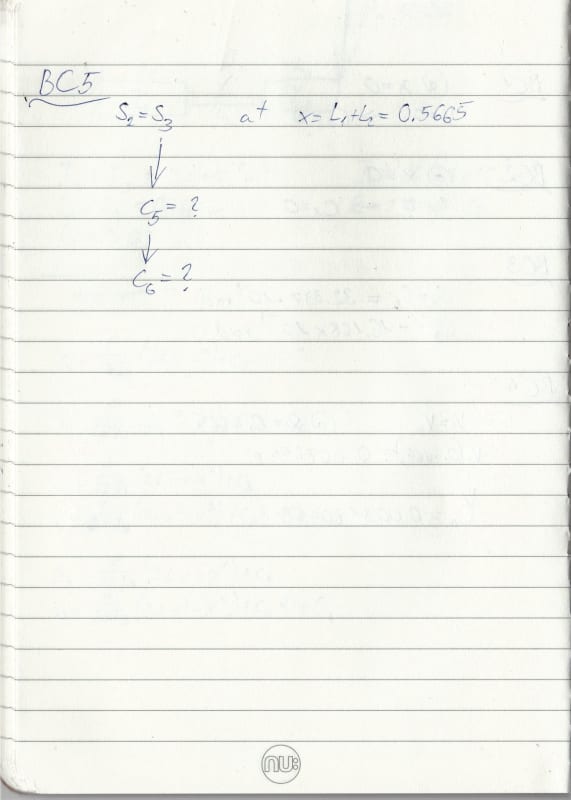
I am trying to calculate the maximum deflection of a beam that has a variable cross-section.
I have tried to follow this method:
However, my beam consists of 3 sections. Therefore, I extended the method shown in the article.
I can't seem to get right the last equation for this problem.
I have plotted my first two equations in MATLAB and they seem to give sensible results (aligned with FEA results).
Can someone check if I am using the right approach, please?