Design of a Flitch Beam using TRADA and Transformed Section methods 3

[As-Lag]

Hello

I am wanting to check the size of a flitch beam. 2 no. 220x45 mm C24 and 200x10 mm S275 plate - 3m long. Generally, I size the beam using the Transformed Section method, transforming the steel to timber. I would normally do my calculations by hand but thought it might be good to "modernise" so I wrote a spreadsheet to do the calculation. As I now use BS1995 for my timber checks, I thought I would use the design method for flitch-beams as described in TRADA Document: GD9 'How to design a bolted steel flitch beam' - ISBN 978-1-900510-54-7. The attached spreadsheet is the result.

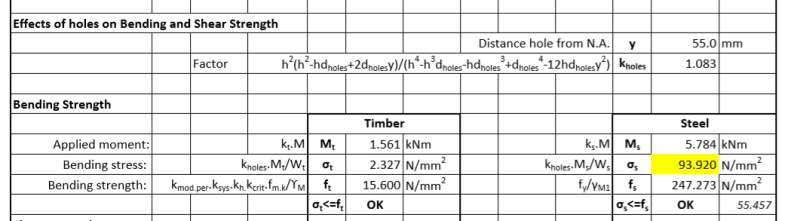
The TRADA design method does not use the Transformed Section but redistributes the load over the timber and steel. There are a number of modifying factors for holes and differences in the E0.05 and Emean values but the procedure is straight forward. Calculate the load distribution k-factors and calculate the bending, shear and deflections using these values of k. I have shown these workings in my spreadsheet. Italic numbers are checks using different calculation methods

However, When I check the stress and deflection using the Transformed Section, I get a very different result with much lower stress values. I also did a steel-plate only check (assuming the plate is held rigid) and I get higher deflection and stress than the transformed section but within expected limits. I have highlighted the results with red numbers as deflection and yellow background as stress.

I know this is a big ask, but where have I made my mistake with the TRADA method? I followed the procedure to the letter and I do not believe the TRADA method would be so out compared with the steel-plate only: so it must be me!

Regards

 

[BAretired]

It is a big ask. Why don't you check your output by hand as you normally do? That is the best way to test a spreadsheet.

BA

 

[BAretired]

Flitch beams should not be designed using transformed sections. Load is distributed to each leaf in accordance with its stiffness.

BA

 

[As-Lag]

Dear BA Retired.

I am totally confused. For years I have been using the University of Michigan's course notes on Flitch Beams (see attached) so I have been educated wrongly. I need to rest a bit.

 

[BAretired]

As-Lag,
Total confusion is no fun and hopefully can be avoided.
I have not read U. of Michigan course notes on Flitch Beams so will make no comment.

Left click the Search function immediately below the thread title. For Keyword(s), enter "Flitch Beam". A number of older threads will appear where Flitch Beams have been discussed on Eng-Tips.

Leaves of a Flitch Beam are held together by bolts. Bolts are adequate to transfer load from one leaf to another but are not adequate to develop composite action. This is important when leaves do not align horizontally.

If a Flitch Beam is carrying a uniformly distributed load of w and there are n leaves, each leaf takes a portion of w according to its own stiffness. So Leaf j takes w(EjIj/ΣEI) where ΣEI in the denominator is the sum of the product of E and I of each leaf for all n leaves.

Please look this over and if you are still confused, let us know.






BA

 

[Agent666]

I second what BA is noting. Rather than being a true composite member transfering longitudinal shears, it's just a sharing of vertical load arrangement. It's no different than attaching two bit of timber together whereby they share the load based on their individual stiffnesses if you applied the load to only one of the timber pieces.

Think of it this way, if you apply load to the timber members in the flitch beam, the majority of the vertical load transfers vertically through the bolts to the steel, virtually none transfers longitudinally due to the oversized holes for bolts (it's free to slip a little between the various plies, negating any true composite action).

The catch is that the timber also creeps under longer term loads, so over time the timber sheds load to the steel. So your stiffness checks under longer term loads should use the longer term timber stiffness.

 

[As-Lag]

You have lost me. I am showing two methods of calculating the stresses in the steel and timber of a flitch beam and there are wide variations. Please read my notes and PLEASE stop surmising my conclusions. The question was: Why such a variation between the methods. My calculations are perfect.

 

[BAretired]

Wow! What a reaction!

L = 3.0m w = 1.24 + 2.0 = 3.24 N/mm
M = 3.24(3000)[sup]2[/sup]/8 = 3,645,000 N-mm

For the case of steel only:
single steel plate 10 x 200
S = bd[sup]2[/sup]/6 = 10(200)[sup]2[/sup]/6 = 66,667 mm[sup]3[/sup]
f[sub]bending[/sub] = M/S = 54.7 MPa

This compares closely (but not precisely) with your value of 55.457 MPa
Edit: My mistake, you had 78.9 MPa for Steel Plate only. Are you using factored load?

What is E for the sawn timber?

BA

 

[BAretired]

Obviously, you cannot have a bending stress of 93.9 MPa when you consider the contribution of the sawn timber.

Now it's your turn! Using the principles that Agent666 and I have expounded, provide E for the wood members and tell us what portion of the total load the steel will carry.

BA

 

[Agent666]

My calculations are perfect.

Maybe, maybe not, I'm not checking them really, but the logic you've based your perfect calculations on is possibly flawed which is what myself and other are trying to say. They could be the best calculations in the world but if you're ignoring whats really occurring then they are still incorrect even if they are perfect.

Why such a variation between the methods.

Because maybe one or both are incorrect. The Michigan method you've link to makes the overarching assumption that the materials are effectively bonded together over the full contact surface. This isn't the case based on what you are proposing, they are free to slip and are fixed with fasteners that can usually deform negating this overarching assumption. Its a matter of load sharing, rather than true composite action.

Someone above noted to go look at some of the other threads over the years on the same subject, they all pretty much come to similar conclusions.

 

[BAretired]

In the above snip, Mt + Ms = 1.561 + 5.784 = 7.345kN-m which is about twice the applied moment. If these values are used to calculate stress in steel, the result will be wrong.

I still do not know what the effective EI is for the timber. I can calculate I = bd[sup]3[/sup]/12 but don't know E. It varies with species and is not very precise in the first place.

BA

 

[Agent666]

BAretired, The material properties are listed on the first page. There's a whole lot of jiggery pokery going on after that on the next page to modify it and so forth for but most of it is related to the adoption of the transformed sections method so isn't to relevant to the point you're probably trying to demonstrate. The moments are amplified I think to an equivalent longer term moment, if you look at the load distribution section, the two values don't even add to 1.0, more like 1.4. So I can only surmise this is factoring things up to account for longer term effects.

What I don't get is that the load in the steel plate in the composite case is higher than just taking the total load and applying it on the steel plate. Ms = 5.784kNm at the bottom of the calculations (this is the moment attributed to the steel plate), yet if you take the factored UDL of 4.674kN/m and work out the total moment over the 3m length M=4.674*3^2/8 = 5.258kNm. This is a physical impossibility I hope the OP will agree!! If the timber sheds all of its load to the steel over time then the moment cannot be higher than the steel plate carrying all of the load!!

The whole approach seems a bit flawed despite the calculations being perfect.

 

[BAretired]

Thanks Agent666; I missed that. I don't understand all the jiggery pokery.
Assuming E[sub]timber[/sub]= 11000 MPa:

EI[sub]timber[/sub] = 11000(2*45*220[sup]3[/sup]/12) = 8.78e11​

EI[sub]steel[/sub] = 200,000(10*200[sup]3[/sup]/12) = 1.33e12​

Sum of EI = 2.21e12​

% of load taken by steel = 1.33/2.21 = 60%
% of load taken by timber = 0.878/2.21 = 40%

Assuming service load of 3.24 N/mm, maximum fiber stress in steel = 32.8 MPa

BA

 

[Agent666]

Yeah that's how I'd typically approach it as well.

For the long term creep to be factored in, simply use the long term modulus of elasticity and do the same calculation. So E_long = E_short/(creep multiplier).

If in this instance the multiplier was 2.0 for creep, then the load ratio would be more like 25%/75%.

So it's important to realise that max timber stress occurs in the short term, max deflection in the long term and max steel stress in the long term. So you sort of have to evaluate both short & long term cases to make sure the flitch beam works over the full spectrum from installation to 50 years in the future after all the creep has occurred and load that was in the timber sheds to the steel.

One other thing is it is important not to simply add the full capacity of the timber and steel, you need to evaluate which one hits it's strength limit first, then back out via calculation based on strain compatibility the stress in the other element. Then knowing the stress you can work out the moment it's carrying. This is a good check to prove the load sharing percentages I guess as well to prove the numbers work out.

I've never come across the situation though where the timber governed in a practical arrangement. It's always the steel plates that govern it.

 

[As-Lag]

Please see attachement. It will answer all your questions.

 

[Settingsun]

Agent666,
The mismatch between the calculated moment on the steel and the total moment from WL/8 is exactly 10%. There's a mention in the TRADA document of increasing the steel's share by 10% to account conservatively for some effects so I imagine this is the source.

As-Lag,
Overall, the Michigan method is quite simple: load evenly shared according to short-term stiffness. TRADA tries to account for effects ignored by Michigan so of course will give larger stresses and larger required beam sizes.

 

[As-Lag]

Firstly, my calculations were not perfect as I found an error in the calculation of ks which I corrected and I attach a corrected pdf. The steel stress is now closer to the stress in the steel alone. My error was with the calculation of ks: I did not multiply the E0.05,fin by It which makes a big difference. Now the percentage distribution is closer to as you all have discussed. Please accept my apologies. Now the calculation shows the steel-plate taking nearly all the load.

With respect to the deflection, the calculation of ks and kt,def require the instantaneous deflection of the timber which I show for mid-span. The calculation required a load factor so I used kt as kt,def did not exist at this stage of the calculation. I have used ks to find the deflection in the flitch.

However, the Transformed Section still shows a marked difference.

Regards

 

[BAretired]

As-Lag,
In your calculation shown above, you say the applied moment is 1.561 kN-m for the timber and 4.484 kN-m for the steel plate. If I add these together, M[sub]flitch[/sub] = 6.045 kN-m (I realize that it is not quite appropriate to add them together).

Moreover, you state that the stress σ[sub]s[/sub] = 72.814 MPa, yet M/S = 4.484e6/66667 = 67.26 MPa where S is the section modulus of the plate.
Edit: Okay, I see that k[sub]holes[/sub] is 1.083, so I see where the stress value came from.

The total applied load, including self weight of the beam is 3.24 kN/m so the total applied moment on a 3.0 m span should be 3.24*3.0[sup]2[/sup]/8 = 3.645 kN-m. If the steel plate carries the entire load, the stress is 54.67 MPa (59.2 MPa with k[sub]holes[/sub] included).

Are you using the factored moment to calculate stress in the plate? Alternatively, how did you arrive at the applied moment?

BA

 

[As-Lag]

BA

Thank you for the time you have taken with my thread. I do use factored moments for strength tests and unfactored for serviceability. I do not use Emean for timber but E0.05.

By checking my answers, I found the error and solved most of my question.

I am onto warping and torsional constants now.

Thanks again

 

[BAretired]

You are most welcome.

BA