Dear fellow researchers,
I am having problems in a Abaqus standard diffusion analysis - water vapour transfer in wooden elements. I ran different analyses:
- mass diffusion analysis of water vapour transfer in wood (using material with defined diffusion coefficients and solubility and surface concentration flux for moisture "load", Fick's law was used for diffusion)
- heat tranfer analysis, using Fourier equations.
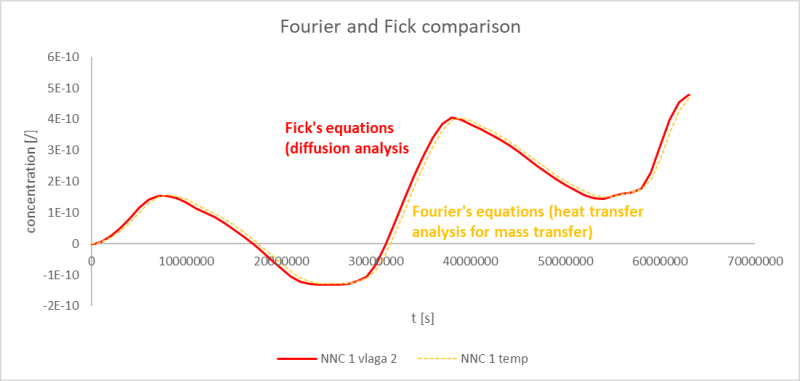
Fourier's equations (25) for heat transfer and Fick's equations (24) for mass diffusion are mathematically analogous.
With the help of research in [1], I set the material characteristics for heat transfer in mass diffusion model, the load was in both cases applied as a factorized relative humidity for 2 years time (cycles of drying and wetting of wood, however the point was just to get the same response with Fourier's and Fick's equations).
The response I got in one point is not the same. Although i got the same range of values (__* 10^-10), the difference factor between both values is around 1.5.
Does anybody got any idea, what else could be wrong? I thank you all for the answers.
With kind regards, Uros
[1] Stefania Fortino, Florian Mirianon, Tomi Toratti: A 3D moisture-stress FEM analysis for time dependent problems in timber structures.
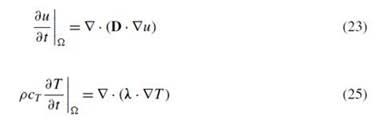
where ρ, cT and T are the density, the specific heat and the temperature of wood, respectively,
while λ represents the second-order thermal conductivity tensor. The analogy between
(23) and (25) is obtained by posing cT = 1 and λ = ρD.
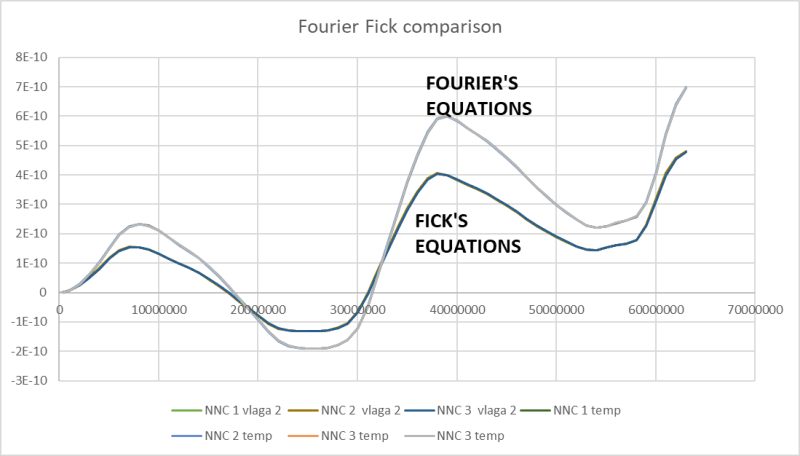
I am having problems in a Abaqus standard diffusion analysis - water vapour transfer in wooden elements. I ran different analyses:
- mass diffusion analysis of water vapour transfer in wood (using material with defined diffusion coefficients and solubility and surface concentration flux for moisture "load", Fick's law was used for diffusion)
- heat tranfer analysis, using Fourier equations.
Fourier's equations (25) for heat transfer and Fick's equations (24) for mass diffusion are mathematically analogous.
With the help of research in [1], I set the material characteristics for heat transfer in mass diffusion model, the load was in both cases applied as a factorized relative humidity for 2 years time (cycles of drying and wetting of wood, however the point was just to get the same response with Fourier's and Fick's equations).
The response I got in one point is not the same. Although i got the same range of values (__* 10^-10), the difference factor between both values is around 1.5.
Does anybody got any idea, what else could be wrong? I thank you all for the answers.
With kind regards, Uros
[1] Stefania Fortino, Florian Mirianon, Tomi Toratti: A 3D moisture-stress FEM analysis for time dependent problems in timber structures.
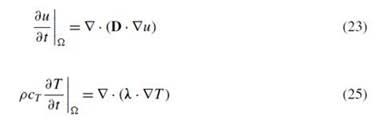
where ρ, cT and T are the density, the specific heat and the temperature of wood, respectively,
while λ represents the second-order thermal conductivity tensor. The analogy between
(23) and (25) is obtained by posing cT = 1 and λ = ρD.