Dissadvantages of using Lagrange multiplier method for contact enforcement? 1

[tugni925]

I am reading the difference between penalty method and Lagrange method for contact enforcement. I am having some trouble understanding how Lagrange works. In the text I found it says Lagrange has the following disadvantages, and I had some clarifying questions;


i. Can make it challenging for Newton iterations to converge

Is it more challenging because it requires more iterations compared to penalty method?

ii. Overlapping constraints are problematic for equation solver

I have read what overlapping constrainsts are (If two tie constraint definitions have part or all of their master surfaces in common), but how does this relate to equation solver, and by equation solver are they talking about for example Newton-Raphson method?

iii. Lagrange multipliers add to equation solver cost

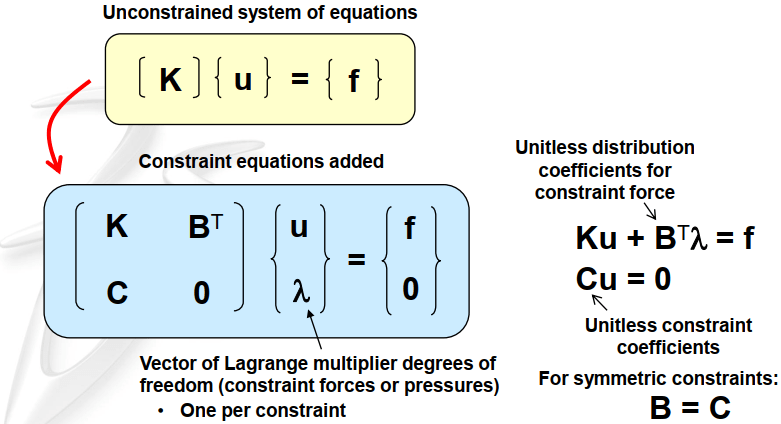
For each constraint, another λ is added to the right vector?

 

[FEA way]

Lagrange multiplier method can cause convergence issues because of sudden changes from zero contact stiffness (when surfaces are separated) to infinite contact stiffness (when contact between the surfaces is established). Also, it increases the computational cost of the analysis because it introduces additional variable for each contact constraint. It's also true that overconstraints can be problematic with this method when they are applied directly to the same DOF for the same set of nodes.

 

[IceBreakerSours]

a) As you can see in the equations in the image, symmetry is broken with Lagrange multipliers. This ruins the positive definiteness of the tangent stiffness matrix (which also increases the computational expense). Most robust implicit solvers were built for symmetric matrices.

Other questions have already been answered above.

*********************************************************
Are you new to this forum? If so, please read these FAQs:

http://www.eng-tips.com/faqs.cfm?fid=376

http://www.eng-tips.com/faqs.cfm?fid=1083

 

[tugni925]

"This ruins the positive definiteness of the tangent stiffness matrix" - would you mind explaining this a bit more IceBreakerSours? The only thing I found was this online: "Positive definiteness of the tangent stiffness matrix guarantees that, when displaced from equilibrium, the structure has the initial tendency to go back to that state."

 

[IceBreakerSours]

Not knowing your background, I can't say if this will make sense but you asked.

At an operational level, three things happen in a structural FE code (implicit solver) -

Displacements -> Strain (kinematics)
Strain -> Stress (constitutive law)
Equilibrium (F=ma)

[Similar operations work across physics.]

Because of these, there is an inherent symmetry in the tangent stiffness matrix - which is required as a starting point for the next (time/load) increment. As it turns out, a symmetric matrix has an "energy" that is convex (bowl shaped) so it is nice for the solvers to go downhill and find an extremum i.e., a converged solution. If the symmetry is broken significantly, then the energy bowl is non-convex and you have all sorts of issues that shows up as poor convergence. If the unsymmetric terms are small in number or relative value, then traditional solvers are robust enough to pull through. Some solvers give users a lot more control over convergence criteria, tolerances, stiffness reformations, line searches, etc. so those knobs can help speed things along but I do not recommend touching those knobs to beginners.

None of this is even a considerationn if you are using an explicit time integrator (e.g., Abaqus/Explicit) because there is no need to assemble a tangent stiffness matrix.

*********************************************************
Are you new to this forum? If so, please read these FAQs:

http://www.eng-tips.com/faqs.cfm?fid=376

http://www.eng-tips.com/faqs.cfm?fid=1083

 

[Mustaine3]

To be fair, general contact and surface-to-surface contact still add unsymmetric terms into the equation, especially when the surfaces are highly curved. The same does friction. That's why I prefer to use the unsymmetrc solver when running a simulation with contact. Abaqus itself will automatically switch to this solver, when the friction coefficient is larger than 0.2.

 

[IceBreakerSours]

Yes, there are several features in codes that break that symmetry. For instance, pressure DOF in hybrid elements and fluid cavities come to mind in Abaqus/Standard; both are coded up as Lagrange multipliers, if I recall correctly.

*********************************************************
Are you new to this forum? If so, please read these FAQs:

http://www.eng-tips.com/faqs.cfm?fid=376

http://www.eng-tips.com/faqs.cfm?fid=1083