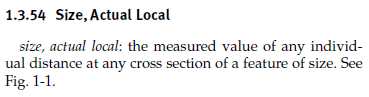Tarator
Automotive
- Sep 20, 2013
- 176
Hi all,
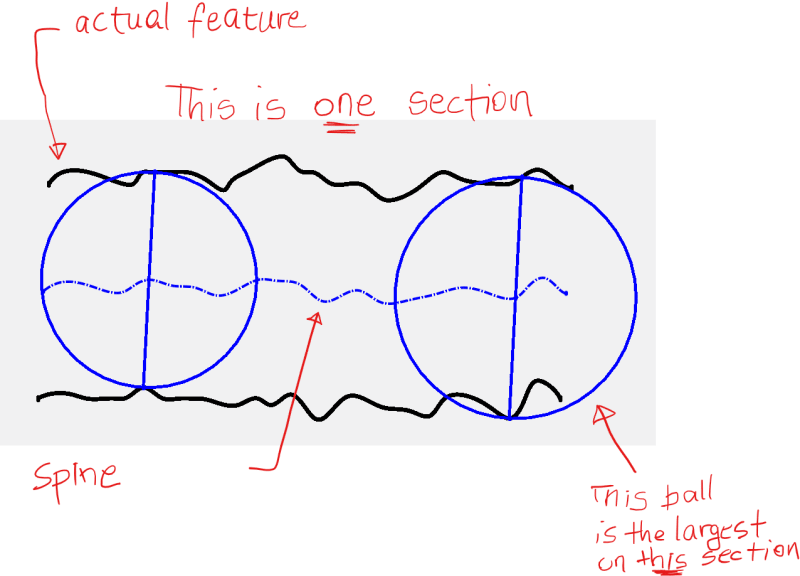
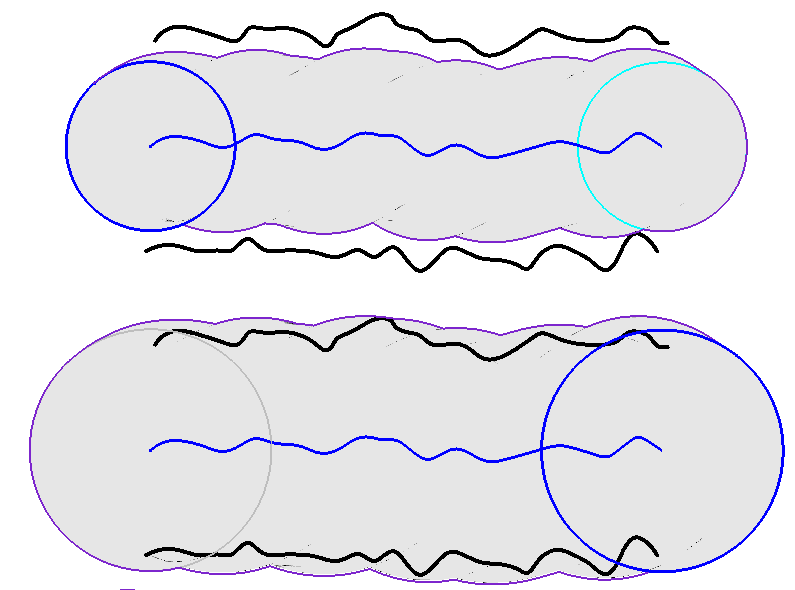
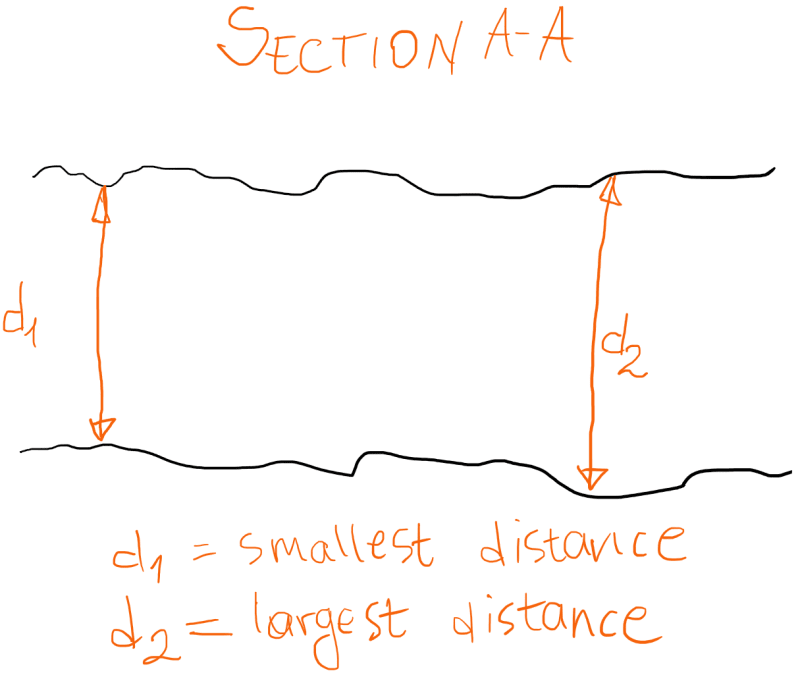
I am trying to understand "spines" as defined in ASME Y14.5.1M-1994 (R2012).
My question is simple: How do you construct your 2 spines (1 for MMC, and 1 for LMC)?
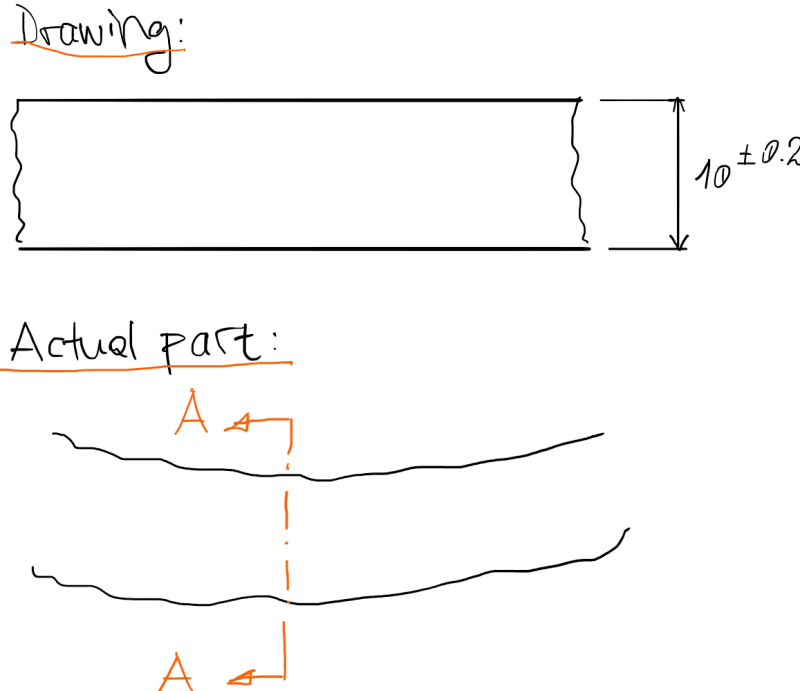
Without the spines, you can't measure your actual local sizes and find the actual MMC and LMC size, in addition to the actual mating size.
I would appreciate it if anyone could shed some light. Thank you.
I am trying to understand "spines" as defined in ASME Y14.5.1M-1994 (R2012).
My question is simple: How do you construct your 2 spines (1 for MMC, and 1 for LMC)?
Without the spines, you can't measure your actual local sizes and find the actual MMC and LMC size, in addition to the actual mating size.
I would appreciate it if anyone could shed some light. Thank you.