user277418
Structural
Hello
Let's pretend that exist a fixed cast-in-place beam 48 m long that is for 100% restrained axially on the ends (externally restrained). From the start of existence the beam is loaded by a load that makes the beam cracked. So it is pre-cracked. The beam starts to shrink and little by little over a long period of time shrinkage strains develop in it. What would be strain distribution in the end of service life of the beam? This is purely theoretical case in sake of curiosity.
Here I am trying to describe the same graphcally
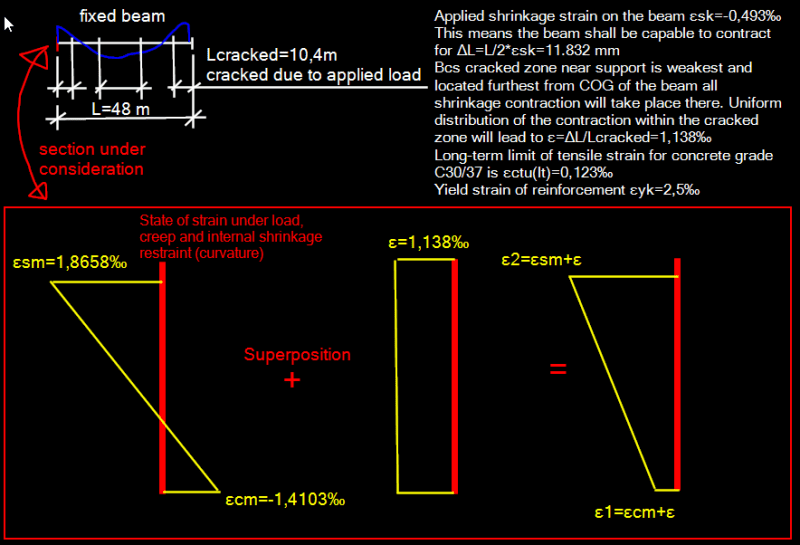
My colleague said that it is incorrect to apply superposition for the case as the beam is cracked. What do you think about that statement?
Also it seems to me distribution of the shrinkage strain by height of the beam is not going to be uniform. This thought is prompted by the fact that axial stiffness of the cracked and uncracked zones are not identical. If you imagine the pre-cracked region of the beam near support as a couple of springs. Reinforcement is a tension spring and uncracked concrete is a compression/tension spring. In my theoretical example approx. stiffness of the uncracked concrete in tension is about 2,5 times larger than of the reinforcement. If shrinkage pulls such set of springs in COG of the beam's cross-section then softer spring will allow more strains to be developed. Which will lead to longitudinal displacement and rotation of the pre-cracked region's cross-sections. This may lead to further opening of cracks in the tension zone of the pre-cracked region, but may not lead to appearing of cracks in compressed zone at all.

I have filling that in the end of service life the beam still shall have compressed and tensioned zones. Even after all shrinkage occurs.
Regards
Let's pretend that exist a fixed cast-in-place beam 48 m long that is for 100% restrained axially on the ends (externally restrained). From the start of existence the beam is loaded by a load that makes the beam cracked. So it is pre-cracked. The beam starts to shrink and little by little over a long period of time shrinkage strains develop in it. What would be strain distribution in the end of service life of the beam? This is purely theoretical case in sake of curiosity.
Here I am trying to describe the same graphcally

My colleague said that it is incorrect to apply superposition for the case as the beam is cracked. What do you think about that statement?
Also it seems to me distribution of the shrinkage strain by height of the beam is not going to be uniform. This thought is prompted by the fact that axial stiffness of the cracked and uncracked zones are not identical. If you imagine the pre-cracked region of the beam near support as a couple of springs. Reinforcement is a tension spring and uncracked concrete is a compression/tension spring. In my theoretical example approx. stiffness of the uncracked concrete in tension is about 2,5 times larger than of the reinforcement. If shrinkage pulls such set of springs in COG of the beam's cross-section then softer spring will allow more strains to be developed. Which will lead to longitudinal displacement and rotation of the pre-cracked region's cross-sections. This may lead to further opening of cracks in the tension zone of the pre-cracked region, but may not lead to appearing of cracks in compressed zone at all.

I have filling that in the end of service life the beam still shall have compressed and tensioned zones. Even after all shrinkage occurs.
Regards
