Eigen-Vectors of the mode shapes

[Zouatine]

Dear Fellow friends,

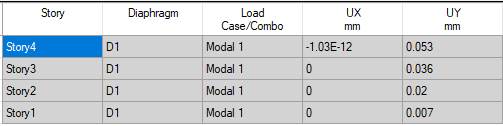
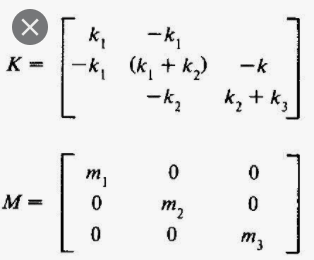
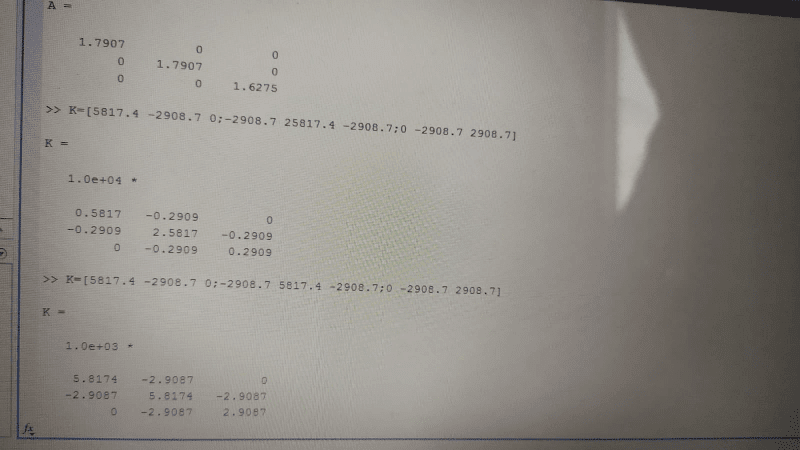
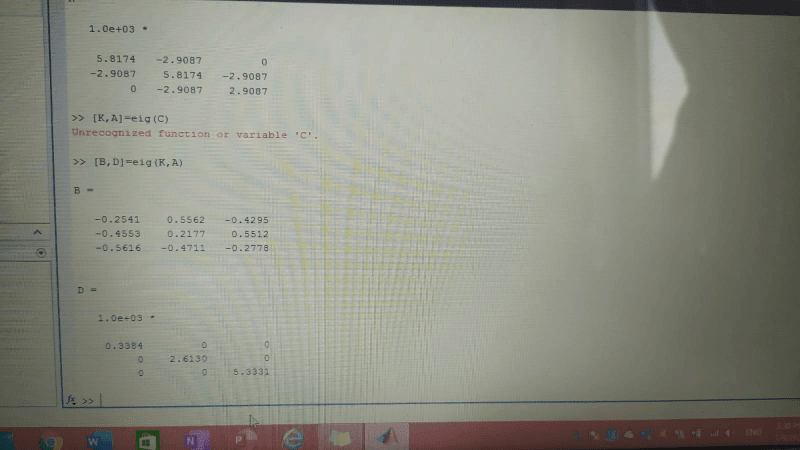
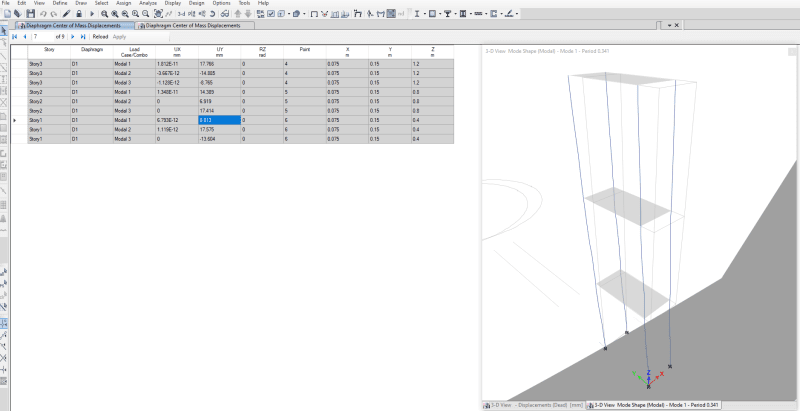
I'm doing a Response Spectrum Analysis for steel Structure (CBF Frame)in Etabs software, however, I'm trying to find the eigenvector noted as ''v'' of the first mode shape for the structure the one that we derive from the formula (K-w^2.M).v=0, I'm stuck in this part I can't find any option to get that.

Thank you for your help ,

 

[wcfrobert]

Hi Zouatine,

Please clarify because there's different level of detail you can get.

1.) Most detailed. I counted at least 136 nodes. If you meshed the slab, then there would be thousands. Each node gives you 6 degree of freedom. That's a size N*6 vector. To get this you need to find the displacement of every node (dx dy dz rotx roty rotz) of your modal deflected shape.

2.) Luckily, usually the software condenses each floor into a single master node at the centroid of the floor plate. Since you have 4 floors, that's a 24x1 vector. To get this, find the displacement of the node at the COM of each floor.

3.) Going even further, sometimes the shear building assumption is taken in which case each master node reduces to 3 DOF (dx dy rotz). That's a 12x1 vector.

4.) Going one step further than that, since the building looks extremely symmetrical, you can neglect torsion and consider a 2D analysis where both orthogonal direction is the same, In this case you only care about the story drift. That's a 4x1 vector.

If you are doing things by hand, option #4 is preferred

 

[Zouatine]

Dear Mr wcfrobert,

Thank you for your reply, sorry if I didn't clarify in my previous post, actually everything is exactly as you said, I mean I do have a symmetrical building, what I'm looking for is an eigenvector with four components each one belongs to each floor, however, when I was checking in the software I found the displacement of each floor ( after considering the center of each floor on the middle by diaphragm option) but the issue with me is how to the transfer the displacement vector to the eigenvector?, in the picture below is the output from the software for the displacement vector.

I was thinking about the hand calculation as you said in the fourth part but the main issue of how to include the effect of the bracing in the global stiffness matrix, when I studied the structural dynamics we included the effect of the diagonal members in the continuum where we have to make a stiffness matric for each element 6x6 matric as well as the mass matric 6x6, but still, my problem in this is how can I do it for 3D structure when I have more than 100 beams.

thank you, I'm waiting for your kind reply

 

[wcfrobert]

I believe the displacement vector IS the your mode shape vector (phi).

The eigen vectors provides the relative "shape" of each mode, the magnitude does not really matter and can be anything as long as the relative shape is maintained (i.e. it can be normalized a number of different ways)

When doing hand-calculation, the vector is often normalize such that phi(1) is equal to 1. In your case: {1; 0.68; 0.38; 0.13}.

Most computer programs compute the mass-normalized shape vector, where {phi}[sup]T[/sup] * [M] * {phi} = .

You can find the mass and stiffness matrix of a shear building pretty quick. The mass matrix is the just a diagonal matrix with mass of each floor, and the stiffness matrix is another diagonal matrix with band width of 3 (with pattern similar to below)

 

[Zouatine]

Thank you for replying to me back Mr wcfrobert,

As far as I understand from your comment that in order to get the eigenvector (the one that we derive from the eigenvalue problem), I have to normalize the displacement vector, as you mentioned {1; 0.68; 0.38; 0.13} so this one is the eigenvector for the first mode shape, am I right for getting your point?

I did a simple hand calculation of three stories frame structure and I checked the values of the time period and I got the same but when I compare the value from the table of diaphragm center of mass displacement after normalizing them, it does not give the same result.

this is the eigenvector from Matlab,

and this is the work from Etabs

and after normalizing them I got V1=(0.733 0.594 0.3308 ) V2= (-0.619 0.28776 0.7309) V3=( -0.3687 0.7325 -0.572)

I'm waiting for your reply , thank you for help