Eurocode: Checking for local buckling in cross section classification vs from buckling curves

[SandorR]

Hello all!

I'm currently learning how to check steel columns against buckling according to Eurocode.

To do this, we first have to classify our cross section. It is done by checking the outstand flanges for local buckling from this chart:

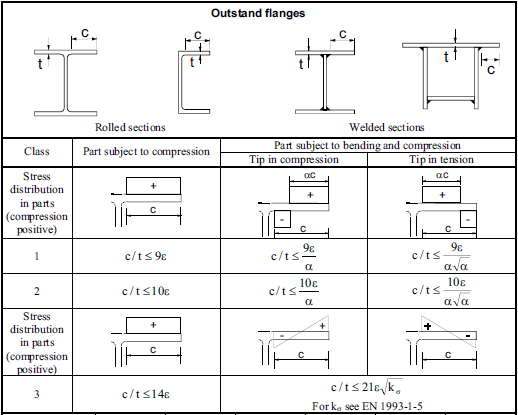
If the cross section belongs to classes 1-3, it means there is no local buckling before yield stress in reached in the extreme fibers of the cross section, and therefore there is no need to reduce the effective cross section area. If the cross section belongs to class 4, then we need to use effective cross section area instead.

Next we need to calculate the column slenderness and use buckling curves to determine the critical load under which the column can be expected to buckle. But before this we need to again classify our cross section, this time to determine to buckling curve A-D to use:

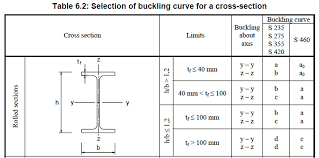
My question is: Why is it necessary to classify the cross section twice? If we first determine the cross section class to be, say, 1, we know that there won't be local buckling before yield and that the whole cross section will be counted into the resistance of the cross section. So why do we need to check it again into a buckling "class"? I see that the buckling curve to be used is dependent again on the slenderness or thickness to width ratio of the flanges. Why is the buckling curve used dependent on the flange dimensions if we have already established that the flanges won't buckle locally?

I know that the buckling curves take other things into account such as the initial curvature of the column, load eccentricity and residual stresses, but taking the dimensions of the flanges implies that the flange slenderness again affects the choice of buckling curve..

Thank you!

 

[Agent666]

The second selection for buckling curve simply recognises that there are different influences of primarily residual stresses depending on flange thicknesses.

The first plate slenderness checks have almost nothing to do with residual stresses, member imperfections, etc.

So in a way the determination of the effective section and the determination of the appropriate buckling curve are not double counting the same effect.