Exponential linear equations 2

[zappedagain]

Can anyone point me to the proper function/procedure to solve this equation for V?

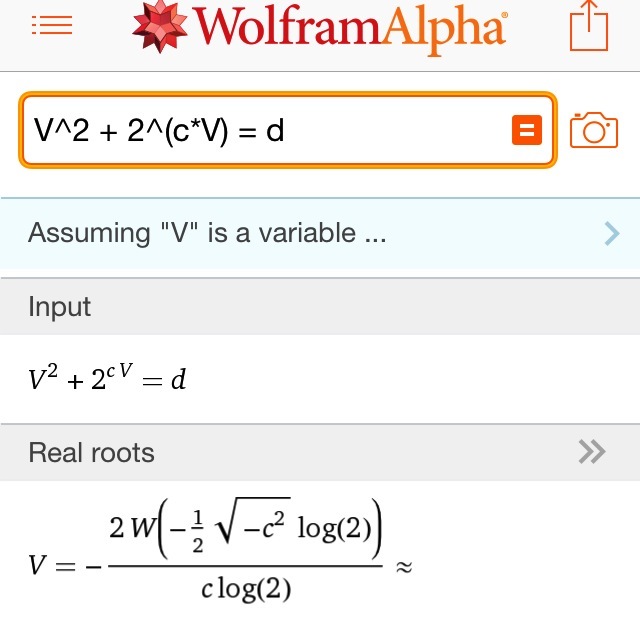
V^2 + 2^(c*V) - d = 0 (so V is added and in an exponent at the same time).

Or am I going to need to approximate it? I'm a bit rusty on the math end.

Thanks,

Z

 

[davidbeach]

Given values for c and d, a MathCad Given-Find block would make quick work of that; the excel solver probably would too. I'm sure there's a different method that my math teachers would find much more elegant, but given the available tools I'd go for brute force.

 

[zappedagain]

Thanks. I tried a Solve in MathCAD 2001. I'll keep digging.

Z

 

[IRstuff]

I doubt there's an analytical solution; it looks too much like a transcendental equation.

I tried Mathcad 15, Maple, Maxima, and an online solver with no solutions to be found.

TTFN
faq731-376

Need help writing a question or understanding a reply? forum1529


Of course I can. I can do anything. I can do absolutely anything. I'm an expert!
There is a homework forum hosted by engineering.com:

http://www.engineering.com/AskForum/aff/32.aspx

 

[Skogsgurra]

That is definitely not an equation you see every day and I doubt, like IR, if there is an analytical solution to it.

What does it describe? A Varistor? Or what? How did you arrive at it?

Gunnar Englund

http://www.gke.org

--------------------------------------
Half full - Half empty? I don't mind. It's what in it that counts.

 

[VEBill]

I entered it into Wolfram Alpha, but with the "- d = 0" trivially modified to "= d", and it offered a V = type solution straight away.

Trying again exactly as presented "... = 0", and it didn't offer up the V = solution.

Now, let me see how to post it...

 

[VEBill]

This is a cropped screen capture posted here using ET's new feature.

The solution shown is "=" and is thus supposedly exact. Further down the page (not included here) it offered approximate numerical solutions.

Wolfram Alpha is, in general, often extremely useful.

Is this solution correct? Best to double check.

 

[Skogsgurra]

Very elegant and convincing!

But, excuse my ignorance, what does W stand for? Is it a secret Wolfram function?

Gunnar Englund

http://www.gke.org

--------------------------------------
Half full - Half empty? I don't mind. It's what in it that counts.

 

[VEBill]

Explanation offered on that is as follows:

"W(z) is the product log function"

Wiki says

http://en.wikipedia.org/wiki/Lambert_W_function

Yikes!! I must have been absent that day.

 

[Skogsgurra]

Yikes!! Absolutely!

And I was obviously absent the whole week!

Gunnar Englund

http://www.gke.org

--------------------------------------
Half full - Half empty? I don't mind. It's what in it that counts.

 

[zappedagain]

Thanks! Interesting how the location of 'd' could confuse the solution. I was wondering if a 'Lambert W' or a 'glog' solution would work; all this new math!

V is velocity for a motion profile that I'm working on.

Z

 

[VEBill]

Typing it that way saved two entire keystrokes!

Laziness (a.k.a. instinctive efficiency) pays off again.

 

[IRstuff]

Oh, yeah, I remember those pesky complex logarithms... You wind up with this lovely corkscrew infinite plane in 3-ish dimensions. My worst class, other than those I flunked outright ;-)

TTFN
faq731-376

Need help writing a question or understanding a reply? forum1529


Of course I can. I can do anything. I can do absolutely anything. I'm an expert!
There is a homework forum hosted by engineering.com:

http://www.engineering.com/AskForum/aff/32.aspx

 

[Skogsgurra]

And the Twiddle Factor! I felt like cheating 'cause I thought it was a Tweak Factor. Who was Twiddle? Or wasn't he/she?

Gunnar Englund

http://www.gke.org

--------------------------------------
Half full - Half empty? I don't mind. It's what in it that counts.

 

[VEBill]

Perhaps one could just plot the curve in a spreadsheet, zoom in on the applicable sections, and extract whatever curve section approximations or numerical data is desired.

If you call that section of the report 'Simulation', then nobody will notice that you skipped the difficult math.

It's a reasonable approach because it only takes a little bit more problem complexity for the equations to become truly unsolvable. Numerical simulation provides much better coverage of the possible problem space.

Probably less susceptible to human error too.

 

[btrueblood]

I like the glogg function approach best for this equation - after you try and solve it, drink some glogg:

http://allrecipes.com/recipe/old-fashioned-swedish-glogg/

 

[geekEE]

Unfortunately it seems like the Lambert W function is not something for which you can easily solve. The Wikipedia page shows that it's only defined as an inverse relation. I think you're still going to need to solve this numerically.