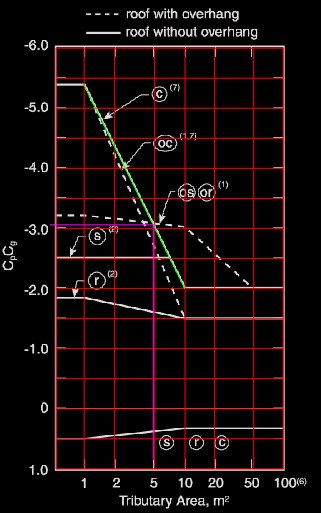
Hey all,
Does anyone know of a resource to find out what the equation for the lines in this graph actually are? Jabacus appears to have a way to calculate it, but I can't find any published equation, and the X-axis is non-linear and non-logarithmic. I've tried fitting some points in excel but I can't get an equation that fits perfectly. I would like to know how Jabacus calculates it; are they interpolating and therefor it's not 100% accurate?
Send help I'm going insane.
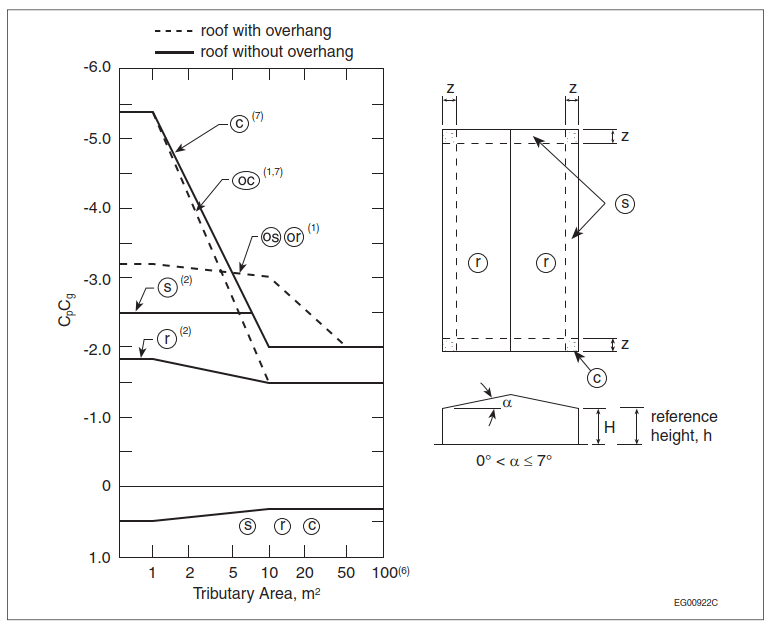
Does anyone know of a resource to find out what the equation for the lines in this graph actually are? Jabacus appears to have a way to calculate it, but I can't find any published equation, and the X-axis is non-linear and non-logarithmic. I've tried fitting some points in excel but I can't get an equation that fits perfectly. I would like to know how Jabacus calculates it; are they interpolating and therefor it's not 100% accurate?
Send help I'm going insane.