MECHENGTOM
Mechanical
- Jan 22, 2025
- 9
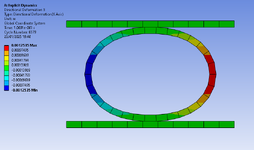
I'm looking for ways in which I can calculate the displacement (vertical and horizontal) of a tube being crushed between two flat plates. I have managed to set up a non-linear material profile and simulate this problem using ANSYS however would like some sort of hand calculation to ensure I am in the correct ballpark. Length of the tube is 0.1 m and a force of 5 kN is applied to the top plate (tube dims and properties as illustrated in the excel spreadsheet image).
I have stumbled across Roark's Formula for Stress and Strain using Table 9.2 Formulas for circular rings however my calculated values are significantly less than my FEA - not sure where I'm going wrong here - Am I missing something to be so far out?

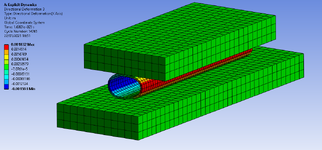
I have stumbled across Roark's Formula for Stress and Strain using Table 9.2 Formulas for circular rings however my calculated values are significantly less than my FEA - not sure where I'm going wrong here - Am I missing something to be so far out?


Last edited: