Tek-Tips is the largest IT community on the Internet today!
Members share and learn making Tek-Tips Forums the best source of peer-reviewed technical information on the Internet!
-
Congratulations cowski on being selected by the Eng-Tips community for having the most helpful posts in the forums last week. Way to Go!
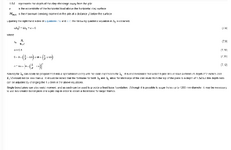
Forces on Laterally Loaded Non-Constrained Piles (2022 CBC Section 1807.3.2.1)
- Thread starter SE2607
- Start date