FREE BODY DIAGRAM - VISE GRIP PLIER

[Gu194]

I ran into a few problems when solving the statics equations of the free body Diagram of these pliers:

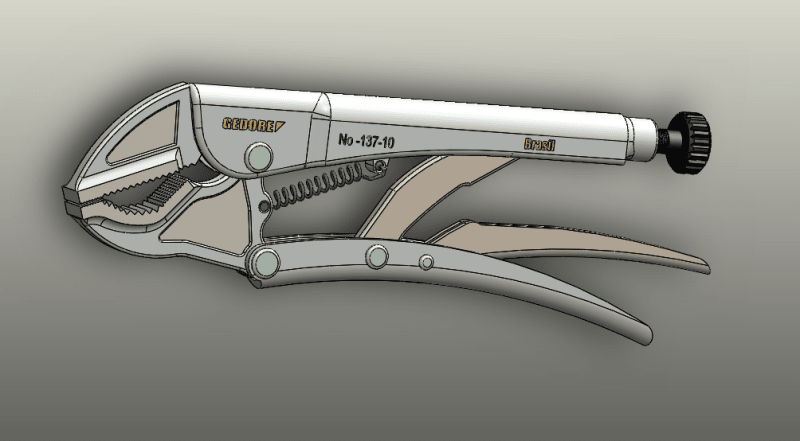
A worker uses these pliers and applies 200 N on it to crush a hex nut. Very basic stuff, the worker does not apply torsion yet. I just want to make sure the diagram is correct.
So I broke it up into the following pieces:

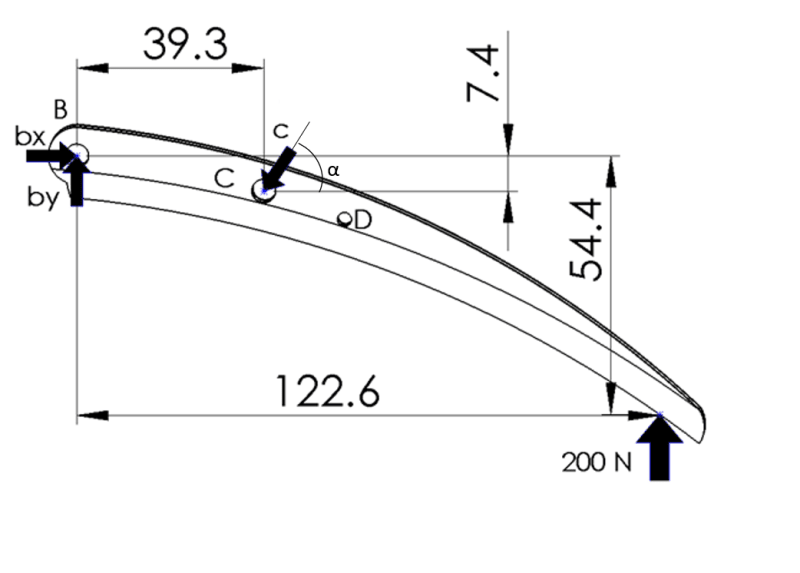
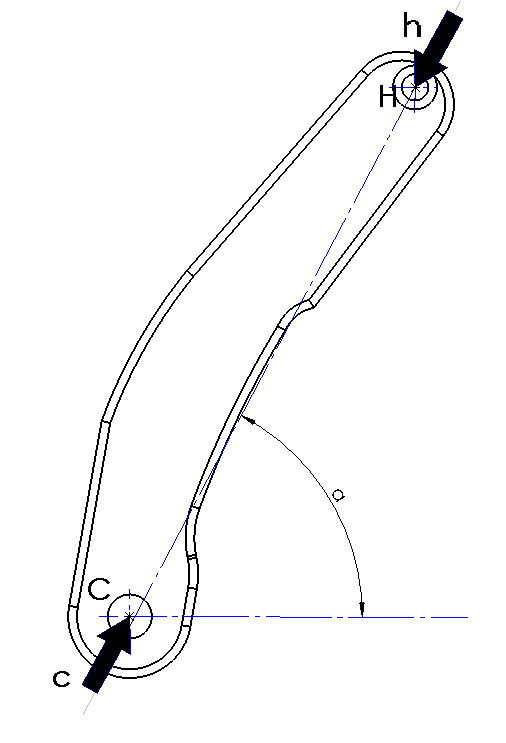
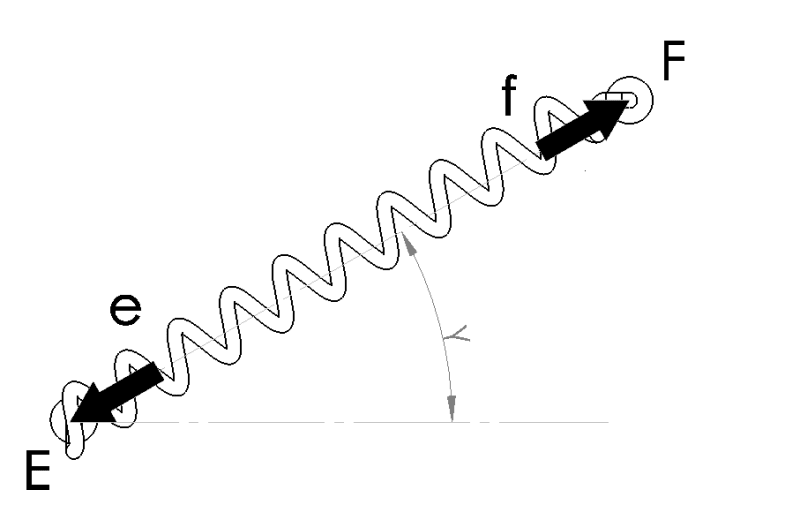
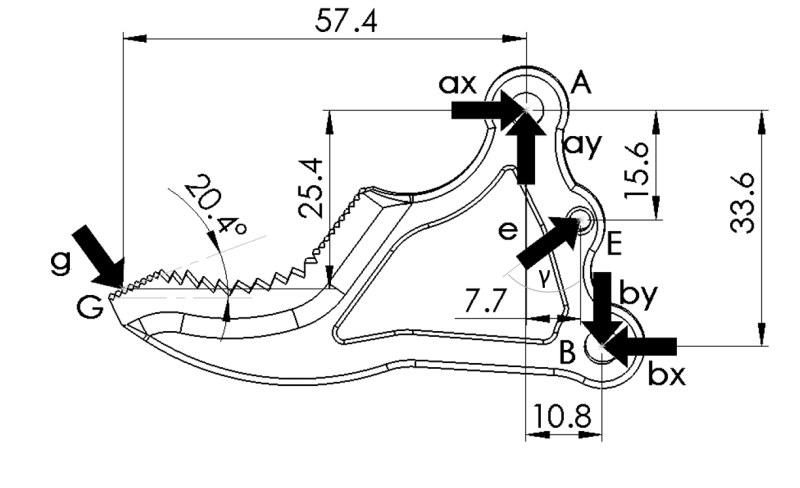
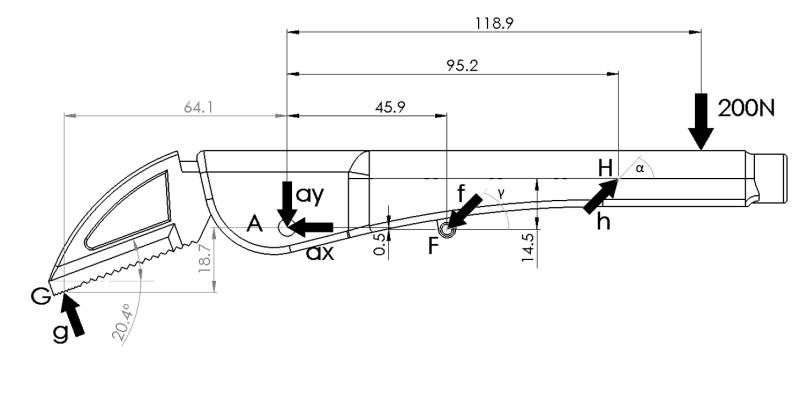
It's modelled on solid works , so i measured everything there(i double checked the measurements).
I ran these equations on MAPLE and this is what I got:

P1 = 200 (N)
∑1Fx = bx - c*cos(α) = 0
∑1Fy = by + P1 - c*sin(α) = 0
∑1MB = by + P1*LBDx - c*sin(α) = 0 # LBDx= lenght from B to D on the x axis

bx= 403.247 by= 347.746 c= 680.173

∑2F = c - h = 0

h=680.173


∑3F = e - f = 0

∑4Fx = -bx + e*cos(γ) + ax + g*sin(20.4) = 0

∑4Fy = - by + ay + e*sin(γ) - g*cos(20.4) = 0

∑4MA = g*sin(20.4)*LAG1y +g*cos(20.4)*LAG1x +e*sin(γ)*LAEx +e*cos(γ)*LAEy-by*LABx -bx*LABy = 0

∑5Fx = -ax + f*cos(γ) + h*cos(α) - g*sin(20.4) = 0

∑5Fy = -ay - f*sin(γ) + h*sin(α) + g*cos(20.4)-P2 = 0

∑5MA = -g*sin(20.4)*LAG2y - g*cos(20.4)*LAG2x - f*cos(γ)*LAFy - f*sin(γ)*LAFx + h*sin(α)*LAFx - h*sin(α)*LAHy - P2*LP2 = 0

F = 1952.786 P2 = 200 , ax = 5338.525 ay= 4413.985
e = -6044.681 f = - 6044.681

The equations turned out fine and balanced, but the results seem a bit too high , and further more , the spring should be in compression and not in tension as demonstrated by the final result of e and f.
I don't understand what I'am doing wrong , but the error seems to be in the last 6 equations if anyone is willing to help me I would mighty appreciate it! Have a look at the Maple if it would help! Any suggestion is welcomed

 

[rb1957]

sum1MB ... no "by" term, "c" term needs arm (suggest using cx*y and cy*x)

are you sure this isn't homework ? (see notes about student posting ...)

another day in paradise, or is paradise one day closer ?

 

[handleman]

Unless the spring is accelerating, e must be equal to f.

 

[electricpete]

dang, vise grips are a lot more complicated than I thought.

=====================================
(2B)+(2B)' ?

 

[LionelHutz]

The spring is always in tension. It's purpose is to hold the jaws open.

I'm not going to try and work through your equations, but the force varies depending on how open (or closed) the handles are. It also varies depending on where in the jaws the part being gripped is. It appears you calculated a constant multiplier?

Also, the picture is not Vice Grips. Vice Grips is a brand name of locking pliers. Most imitators suck compared to real ones.

 

[handleman]

If you really want to get pedantic, this is a viCe grip:

Otherwise, ViSe Grip is indeed a brand name, but it's like Kleenex. It's become standard usage.

 

[LionelHutz]

Most any tissue can do the job when blowing your nose. Lots of the Vice Grip imitators are so useless you're better off throwing them in the scrap.