Head Pressure Loss

[BracketMan55]

Hello all, I am a mechanical engineer working on a very particular application involving a fluid pump required to supply cleaning fluid (could be cleaning solution or just plain water) to a set of nozzles at the top of an 80 foot elevation. Attached is a layout of the overall system design overview.

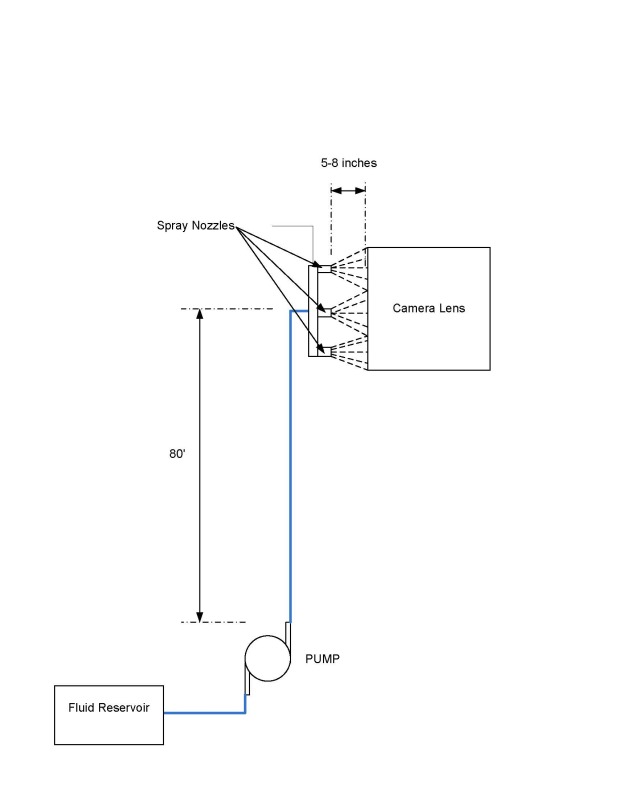
In particular, we have a pump supplying pressure up a rubber hose to an elevation of approximately 80 feet. The fluid is then fed through a manifold and then sprayed through some nozzles to apply a cleaning action to a camera lens.

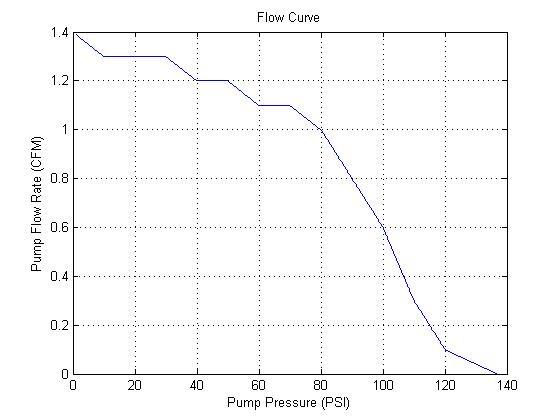
My question regarding this, however, pertains to the how we have been testing this set-up. In particular, we wanted to figure out if the pump we had was of a sufficient pressure to supply the cleaning fluid up the 80 foot elevation through the hose and then through the nozzle set-up such that it could provide a high enough spraying velocity to sufficiently clean the nozzle. When we did our testing, however, we did not have 80 feet of elevation to test the set-up in its desired configuration. It was then decided that a pressure regulator could be employed to drop the pressure in the hose by such an amount as to account for the 80 feet of head loss due to the elevation. Our question is, is this a valid approach? That is, is it justifiable from a scientific and engineering stand-point to simply exchange 80 feet of head for a pressure drop via a pressure regulator in the line (since we are using Bernoulli's equation to model this system for a compressible flow)? Does exchanging the head pressure for a pressure regulator cause any decrease in the velocity of the flow inside the line or a decrease in the flow rate? Also, does this exchange adversely effect the system curve in a way as to effect the flow rate? I have the pump curve for the pump we are using attached.

Thanks for all the help and expertise folks!

-Bracket Man

 

[bimr]

Yes, you may simulate the pressure with a pressure regulator. The pressure will be effected, not the flow.

 

[LittleInch]

Is it a valid approach? Yes

It is justifiable. What you really need to do is make the valve have a fixed pressure drop across it of about 35 psi (assuming you have no head change between pump and nozzles rather than a fixed pressure) which is the equivalent of 80 ft. That will simulate the static head better.

The velocity will be the same in this case as it would be in the final case.

It won't affect the pump curve any more than it would be if the pressure drop was due to static height rather than a control valve. The flow will be where the system curve meets pump curve. All depends on the losses through your spray nozzles, but looks like you'll have at least 40 psi to play with.

Bernoulli isn't a great way to calculate flow like this though.

Remember - More details = better answers
Also: If you get a response it's polite to respond to it.

 

[BracketMan55]

Thanks for the info in the reply! One quick question, and please don't think me too much of a novice for asking this if it is common mechanical engineering knowledge, but why is Bernoulli not a sufficient way to model this kind of flow?

-Bracket Man

 

[LittleInch]

Generally because it ignores friction. There are much better equations for liquid flow which take account of it.

Remember - More details = better answers
Also: If you get a response it's polite to respond to it.

 

[BracketMan55]

Yes, but in the fluid mechanics book that I have (by Fox and McDonald) they give an equation that can be substituted within Bernoulli's equation that gives the frictional losses.


hl = Frictional Losses = f*(L/D)*((V^2)/2) where f is the friction factor, L is the pipe (or for our case hose) length, D is the pipe (or for our case hose) diameter, and V represents the average velocity of the flow. In Bernoulli's equation, the frictional losses can be represented as the following:

(((P1/(rho*g)) + (alpha1*((V1^2)/(2*g))) + z1)) - (((P2/(rho*g)) + (alpha2*((V2^2)/(2*g))) + z2)) = hl

Is this not a correct representation?

 

[LittleInch]

I'll leave it to others to fill in the issues here, but it's not a great way to work out real life fluid flow like this.

Remember - More details = better answers
Also: If you get a response it's polite to respond to it.

 

[dicksewerrat]

When you pressurize the hose, is it expanding? And using 80 feet of hose in your test? A 5% increase in the hose diameter throws thing out. different flow rate, maybe a smoother hose wall,

Richard A. Cornelius, P.E.

http://WWW.amlinereast.com

 

[Artisi]

What is the big deal- stick the 80ft of hose into the test system and run the pump, problem solved - no academic discussion needed, no guess work - pump performance will be established in terms of nozzle flow and pump discharge pressure.

It is a capital mistake to theorise before one has data. Insensibly one begins to twist facts to suit theories, instead of theories to suit facts. (Sherlock Holmes - A Scandal in Bohemia.)