DoubleEngineer
Mechanical
- Sep 23, 2009
- 9
Hello,
Here is my situation:
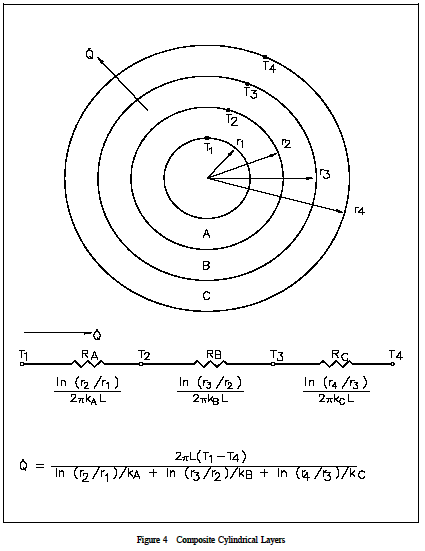
A hollow multi layed concentric cylinder that is placed inside a vacuum. There is a heating element in the middle of the cylinder.
Temp initial is room temp and the pressure initial is atm.
Temp is increased to 350 degs C. Pressure is reduced to about 40 milliTorr.
I have calculated the Heat Transfer for atmospheric pressure but can not seem to find enough information about thermal conductivity of different materials at vacuum pressures.
Could anyone tell me an equation for thermal conductivity of materials at vacuum pressures.
Basically, im trying to figure out an ideal pressure for my system, that is still in a vacuum, and to determine the differences between heat transfer if 1) the heating element is placed on the inside of the cylinder or 2) at the outside around the cylinder.
Thanks for any responses,
DoubleEngineer
Basic Problem--
Here is my situation:
A hollow multi layed concentric cylinder that is placed inside a vacuum. There is a heating element in the middle of the cylinder.
Temp initial is room temp and the pressure initial is atm.
Temp is increased to 350 degs C. Pressure is reduced to about 40 milliTorr.
I have calculated the Heat Transfer for atmospheric pressure but can not seem to find enough information about thermal conductivity of different materials at vacuum pressures.
Could anyone tell me an equation for thermal conductivity of materials at vacuum pressures.
Basically, im trying to figure out an ideal pressure for my system, that is still in a vacuum, and to determine the differences between heat transfer if 1) the heating element is placed on the inside of the cylinder or 2) at the outside around the cylinder.
Thanks for any responses,
DoubleEngineer
Basic Problem--

