I have been struggling with a problem I got from my professor as I firmly believe his solution is wrong, but I cannot find a correct solution to show him.
A first-order exothermic reaction A -> B takes place in a tubular reactor (typical PFR). The tube is cooled to a constant wall temperature 𝑇𝑤 and the total amount of heat removed from the reactor is given (𝑄, in Watts). All needed constants and geometrical parameters were given, as well as 𝑇𝑖𝑛𝑙𝑒𝑡 and 𝑇𝑜𝑢𝑙𝑒𝑡. The goal is to find the (constant) value of the wall temperature 𝑇𝑤 that ensures 𝑄 is being removed from the entire length of the reactor.
My question is not so much about the final number, but rather the logic to get there. In my professor's official solution, they simply used the following formula from a heat exchanger:
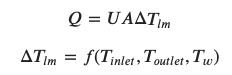
where Δ𝑇𝑙𝑚 is the logarithmic mean temperature difference. 𝑄, 𝑈, and 𝐴 are given in the question. One would then isolate 𝑇𝑤 and solve for it, as all other values are given.
This formula is easily derived from a simple heat exchanger, but as soon as a chemical reaction is happening inside the inner duct, the energy balance doesn't result in this aforementioned equation anymore as there is now a term for the enthalpy of reaction in the balance.
The reactor heat balance in this scenario would be:
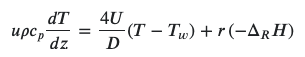
where Δ𝐻 is the reaction enthalpy, 𝑟 is the reaction rate, 𝐷 is the reactor diameter and 𝑧 is the main axis-coordinate of the reactor, assuming there's no temperature profile radially. 𝑈, 𝑢, 𝜌, and 𝑐𝑝 are heat transfer coefficient, flow velocity, specific mass and heat capacity, respectively.
If the reaction were non-existing (𝑟=0), one could derive the mean-log approach to solving this from the balance above. But that's not the case in a chemical reactor.
Do you believe this problem is solvable? I would try to numerically solve the energy balance above but I don't have 𝑇𝑤 to begin with so I don't know how I could tackle this simulation. If my professor's approach is correct, why can't I derive that formula from the energy balance? I've looked through textbooks in three different languages and couldn't find a single instance of mean-log temp. approach being used to determine anything in a cooled/heated tubular reactor.
Thanks a lot for any input!
Best regards.
A first-order exothermic reaction A -> B takes place in a tubular reactor (typical PFR). The tube is cooled to a constant wall temperature 𝑇𝑤 and the total amount of heat removed from the reactor is given (𝑄, in Watts). All needed constants and geometrical parameters were given, as well as 𝑇𝑖𝑛𝑙𝑒𝑡 and 𝑇𝑜𝑢𝑙𝑒𝑡. The goal is to find the (constant) value of the wall temperature 𝑇𝑤 that ensures 𝑄 is being removed from the entire length of the reactor.
My question is not so much about the final number, but rather the logic to get there. In my professor's official solution, they simply used the following formula from a heat exchanger:
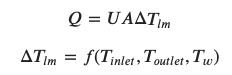
where Δ𝑇𝑙𝑚 is the logarithmic mean temperature difference. 𝑄, 𝑈, and 𝐴 are given in the question. One would then isolate 𝑇𝑤 and solve for it, as all other values are given.
This formula is easily derived from a simple heat exchanger, but as soon as a chemical reaction is happening inside the inner duct, the energy balance doesn't result in this aforementioned equation anymore as there is now a term for the enthalpy of reaction in the balance.
The reactor heat balance in this scenario would be:
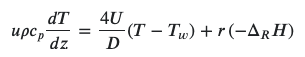
where Δ𝐻 is the reaction enthalpy, 𝑟 is the reaction rate, 𝐷 is the reactor diameter and 𝑧 is the main axis-coordinate of the reactor, assuming there's no temperature profile radially. 𝑈, 𝑢, 𝜌, and 𝑐𝑝 are heat transfer coefficient, flow velocity, specific mass and heat capacity, respectively.
If the reaction were non-existing (𝑟=0), one could derive the mean-log approach to solving this from the balance above. But that's not the case in a chemical reactor.
Do you believe this problem is solvable? I would try to numerically solve the energy balance above but I don't have 𝑇𝑤 to begin with so I don't know how I could tackle this simulation. If my professor's approach is correct, why can't I derive that formula from the energy balance? I've looked through textbooks in three different languages and couldn't find a single instance of mean-log temp. approach being used to determine anything in a cooled/heated tubular reactor.
Thanks a lot for any input!
Best regards.
