Height Needed To Enter Pipe 1

[fyrefreezer]

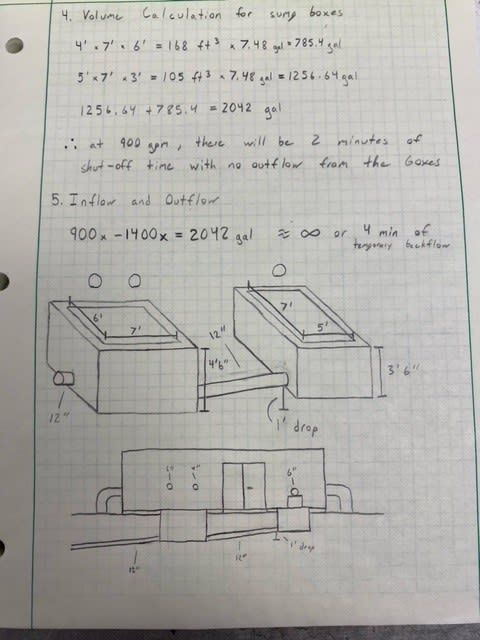
How can I translate the height of water in a box to the velocity needed for a water to enter a pipe? Assuming all this work is being done by gravity, no pumps.

I have came to the conclusion of the Bernoulli Equation to get sqrt(2*g*h) = v^2

Would this actually be able to translate into the velocity that the water is moving? How could I find the velocity I would need to enter the pipe in the first place?

 

[cvg]

typical entrance loss is 1/2 the velocity head

https://www.hec.usace.army.mil/conf...for the coefficient gives a higher head loss.

 

[LittleInch]

Fyre freezer,

When you start a second post about something you've already got another post running on then it's normal to provide a link to it so that people don't go asking the same questions.

Like this

https://www.eng-tips.com/viewthread.cfm?qid=496649

I'm not following your calculations and not quite sure what you're trying to find. I do know that Bernoulli is often not the best tool.

For your 900 GPM in your sloping 12" pipe, I think the issue is how full does the pipe get and what are you looking at in terms of open channel flow.

Once your pipe starts to get 80-90% full then you risk getting slugging and surging until the flowrate means you're running a full pipe nearly all the way.
So figure out first what type of flow you have in your 12" pipe - open channel, full or some mixture of the two

Remember - More details = better answers
Also: If you get a response it's polite to respond to it.

 

[fyrefreezer]

@LittleInch Thanks for letting me know I am new to this forum page, it was a separate question so I thought I should make a new thread, since it also has some different details.

The type of flow I'm assuming would be a partially full flow around 64% full if I use that 900 gpm is coming into the box at a time and the capacity of the 12" is 1400 gpm. 900/1400 = 64% Why would it matter how full the pipe gets assuming its satisfying the incoming flow amount?

I just want to find how much pressure/velocity/height of water is needed for the water to move down the pipe at some lower point and the formulas to figure that out. Is there even a need to calculate this?

The calculations I provided are for the flow of the sloped 12" drain using hazen, and mannings partial flow. My attempt at trying to find the velocity/height needed for flow down the drain. The volume I would have between the two boxes and how much time that would give if there was zero flow down the 12" drain and the inflow, outflow calculations assuming my flow calculations are correct.

I might be trying to design this totally wrong or something, so if I am please let me know how I should go about it instead.

 

[katmar]

There is an article titled "Designing Piping for Gravity Flow" by PD Hills which was published in Chemical Engineering, Sept 5, 1983, pgs 111-114. It deals with unflooded outlets which can be either in the base or side of a tank and it provides curves which allow you to calculate the head required to achieve a certain flow rate in near horizontal piping.

Because it is rather old, not many libraries have digital copies but you will find scans made from old photocopies floating around the web. IMO it is very valuable in developing an understanding of gravity and self venting flow. It's well worth making the effort to get a copy.

Katmar Software - AioFlo Pipe Hydraulics

http://katmarsoftware.com

"An undefined problem has an infinite number of solutions"

 

[1503-44]

H = v^2/2/g + entry loss

Einstein gave the same test to students every year. When asked why he would do something like that, "Because the answers had changed."