Robert Clark
Aerospace
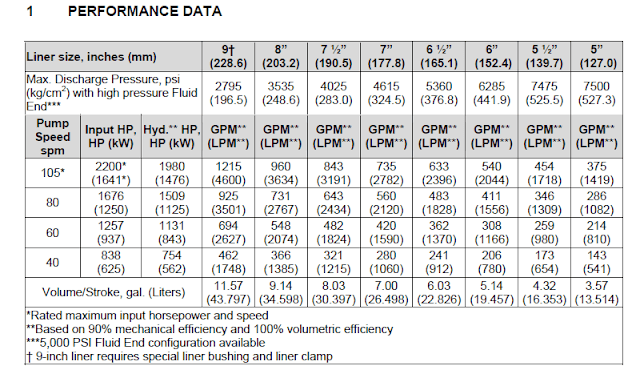
A pump’s power is a product of its pressure rise times volume flow rate. Commonly, a pump is specified by giving the pressure rise, or head, it can provide and the flow rate, such as in gallons per minute(GPM).
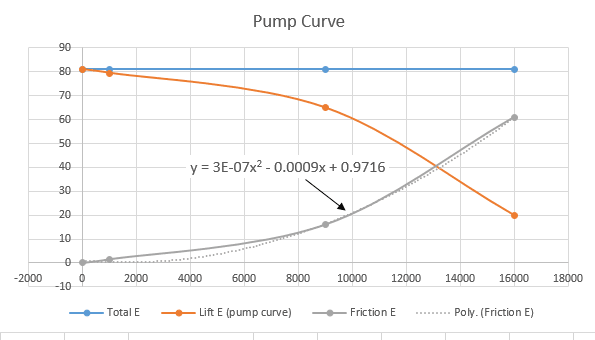
But some pumps provide the user with a chart that shows how the pressure rise can be varied with a corresponding change in flow rate, inversely related.
This is what I need for my application. I need a higher head than what the specs say for the pump, allowing for the reduced flow rate. The specs don’t say whether or not these values can be varied. So is there some common method by which this is done for pumps with this capability?
I thought they just reduce the inlet size to change the flow rate, with an associated change in the size of the pressure rise. But then I thought this would just mean the pump would just suck harder on the water input source, making the flow rate stay the same.
So how do pumps with this variable capability do it, and can other pumps be adapted to also do it?
Robert Clark