Pen_theApprentice
Mechanical
- Nov 25, 2024
- 2
Good morning engineers!
I'm tring to create a logarithmic spiral driven by equations.
the general equation for that is:
r=ae^(b*θ)
and I converted this equation in terms of y, z, so i can determine the coordinates in cartisian system:
y=a*e^(b*θ)*cos(θ)
z=a*e^(b*θ)*sin(θ)
a, b and θ are pre created parameters in that part.
The problem is, as in law editor, only two variables can be involved as i know,
how can I work this out?
thank you!
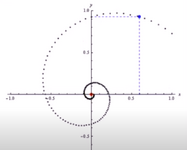
I'm tring to create a logarithmic spiral driven by equations.
the general equation for that is:
r=ae^(b*θ)
and I converted this equation in terms of y, z, so i can determine the coordinates in cartisian system:
y=a*e^(b*θ)*cos(θ)
z=a*e^(b*θ)*sin(θ)
a, b and θ are pre created parameters in that part.
The problem is, as in law editor, only two variables can be involved as i know,
how can I work this out?
thank you!

