I Need a Concrete Cross Section Analysis Tool that May Not Exist 2

[KootK]

I would like a tool that would allow me to determine the moment of inertia of the cracked, transformed section of the shear wall group below for a given location and angle of the neutral axis. I know, it's asking a lot. Anybody know of such a thing? Our own member Denial has something close for arbitrary solid sections but I don't believe that would handle the voids.

 

[Celt83]

PCA Column can handle that.

IDS may have a spreadsheet but I'm not certain about the voids

This tool looks promising but again not sure on the cracked transform aspect:

https://github.com/robbievanleeuwen/section-properties

developed by HandoftheLion

I've got my self on only the beginnings of P/M curve stuff for concrete columns which would need a method similar to what your asking.

Edit: I have what I think would be the process sketched down
- define the outer perimeter of what would be the solid column with vertices in counter-clockwise order (think this gives you a + signed area)
- define the inner voids with vertices in clockwise order (signed area ends up opposite)
- define all the bar coordinates and areas
- transform the section + bars so the desired netrual axis angle lies on the horizontal
- find the edge intercept points with the neutral axis within the bounds of the vertices (kind of do this in my drift program and did something similar in a function I axed cause the end results were too far off...maybe could be reporposed..line 150 to line 256 here:

https://github.com/buddyd16/Structu...7c899e#diff-10e555fff839d33699d84b504dc41230)

- do parallel axis theorem for the moments of inertia of all the areas, using their signed areas (void properties will subtract)
- transform properties from the current local axis back to the global axis (hmm maybe don't need to do this part if you are interested in the moment of inertia about the neutral axis angle)

Open Source Structural Applications:

https://github.com/buddyd16/Structural-Engineering

 

[JoshPlumSE]

Well PCA column doesn't exist anymore. It's now Structure Point, SP Column.

I was going to add that the regular PCA column probably can't do this and you'd have to get the "Irregular Column" version to do it. But, it looks like the two programs have been merged together for Structure Point's SP Column.

 

[Denial]

KootK,

My spreadsheet should handle voids.[ ] You just need to traverse the outer surface anti-clockwise, then nip through the thickness of the concrete to the inner surface, then traverse the inner surface clockwise, then nip back to your starting point on the outer surface.

You can partially confirm that it works OK by setting up a relatively simple hollow shape with linear material properties.[ ] You can also run the "Tweaker" macro (Ctrl-Shift-T) before doing the actual analysis and set the Tweak Level to 2.[ ] Then at the end of each load case you will get (among other stuff) the "marginal section properties" for the load case.[ ] The Tweaker macro is described on the Documentation worksheet.

 

[KootK]

Thank you all.

PCA Column can handle that.

Can it? This was my first thought too but, based on the feature list that I found on line, I suspected that output stopped at reporting neutral axis location. If that's so, it might be some painful post-processing after that.

...then nip through the thickness of the concrete to the inner surface...

Thanks much. I'm utterly ashamed of myself for not thinking of this. My attempt at a similar thing in MathCAD works the same way.

 

[Guest262653]

Have you tried Sbeton from Blue5soft? It covers general sections and is free for 90 days.

http://blue5soft.com/en/sbeton/

 

[Huevo]

PCA Column can handle that.

Can it? This was my first thought too but, based on the feature list that I found on line, I suspected that output stopped at reporting neutral axis location. If that's so, it might be some painful post-processing after that.

Just checked, spColumn can't handle more than one opening.

 

[Agent666]

KootK

You are also correct that SPcolumn and PCAColumn only reports the neutral axis depth and maximum steel strain at the ULS, as its only basically setup to work out the ultimate capacity of a member and nothing more. It does a good job of this.

In SPColumn you can only have a single opening defined, but you can use the same trick with a thin nip through the thickness to create more. You can analyse any arbitrary arrangement, though the built in drawing tools are pretty limited, but you can import text based data on section and reinforcement coordinates provided its in the correct format. So its pretty easy to link into spreadsheets that output a text file in the correct format, import this and run analysis. With a spreadsheet setup correctly its much quicker to use than using the inbuilt tools which are pretty cumbersome as soon as you go to irregular sections or reinforcement layouts (think manually inputting coordinates one at a time in a tiny window that cannot be resized).

Attached is a example of the output, its pretty basic stuff, but all ULS or gross section related properties I'm afraid.

 

[IDS]

The spreadsheet linked here:

https://newtonexcelbach.com/2014/06...nder-combined-axial-load-and-biaxial-bending/

does ULS bending + compression design for biaxial bending for any cross section defined by corner coordinates. You enter the axial load and moments about the X and Y axes, and it calculates the NA location and angle, and ULS bending capacities (to Australian and Euro codes only, sorry).

I haven't checked it properly with multiple voids, but it should work OK, using the anti-clockwise entry for voids.

p.s. One of my files here had a VBA problem, associated with calling microtimer. Let me know if you have any problems with the download version.



Doug Jenkins
Interactive Design Services

http://newtonexcelbach.wordpress.com/

 

[Celt83]

I've made some headway on my end...I recently uploaded a new section props script that generalizes closed polygons much better than the GUI program I've had up there does. In the newer script you can specify a section as a void or solid and transform the properties based on an n = Emat1/Emat2.

Individual pieces I have left:
given a bisecting horizontal line determine the sub closed polygon above it. (I want to solve this more generally so the bisecting line can be at any angle and I can get the created closed sub polygons on either side of the line.)

In pseudocode:
[ul]
[li]define the concrete solid shape[/li]
[li]define the concrete voids[/li]
[li]define the bar locations[/li]
[li]define n = Es/Ec[/li]
[li]get the required N.A. rotation[/li]
[li]rotate the coordinates about the geometric centroid so the N.A. would be horizontal[/li]
[li]find the N.A. depth for the cracked section - moment of transformed area above the NA about NA = moment of transformed area below the NA about the NA. Bar area below the line is n*As and bar areas above the line are (n-1)*As. Since the solution for the N.A. in this instance lies within the bounds of the transformed shape the bisection method should work for this so starting with the N.A. at the highest point shift it down until we find the right location.[/li]
[li]determine N.A. line intersections with concrete solid edges[/li]
[li]determine N.A. line intersections with concrete void edges[/li]
[li]create the concrete solid sub polygon above the N.A.[/li]
[li]create the concrete void sub polygon above the N.A.[/li]
[li]determined second moment of area for the axis of interest for the new trimmed composite section (see below may need to transform back to geometric axis depending on what result your after)[/li]
[/ul]

edit:

Do want Icracked about the neutral axis angle you chose or the neutral axis that aligns with the bending direction? This is the snag I run into on biaxial columns since the neutral axis angle varies to keep you on the same P-M isocline.


Open Source Structural Applications:

https://github.com/buddyd16/Structural-Engineering

 

[Guest262653]

I ran an example in Sbeton with a two holed RC section and using Canadian standards.
I attach the report file, a screen capture of a moment-curvature relationship and the input files. Hope it helps.

 

[Celt83]

give this a try:

https://github.com/buddyd16/Structural-Engineering/blob/master/Analysis/eng_tips_maybe.py

you'll also need the section_props.py file in the same folder.

sample output:

Open Source Structural Applications:

https://github.com/buddyd16/Structural-Engineering

 

[Celt83]

and with the two voids:

Open Source Structural Applications:

https://github.com/buddyd16/Structural-Engineering

 

[Agent666]

Hi Celt, have not looked through the code yet (mostly work in VBA but learning python is definitely on my bucket list). But will it handle this situation and isolate all the horizontal slices of the section for subsequent processing (I assume this is how you are doing it based on the pseudo code)? The screenshots you have posted so far are resolved into simple triangles only). I started doing something similar for ULS design years ago but ended up giving up as there were a few situations where my approach didn't quite work and I never quite got to the bottom of it.

This was about the trickiest thing I could image given your test section.

 

[Celt83]

yup was a royal pain the rear:

for fun:

Open Source Structural Applications:

https://github.com/buddyd16/Structural-Engineering

 

[Celt83]

C:

and with a flat segment on the cut line:

Open Source Structural Applications:

https://github.com/buddyd16/Structural-Engineering

 

[Agent666]

Champion!

Looking through the code, you'd probably get by with half as many iterations to find the neutral axis if you implemented a root finding method like Brents Method in place of using the bisection method (based my own experience). No idea how many iterations its taking or how computationally expensive this process is, but implementing brents method in some of my own personal spreadsheets definitely increased the speed of convergence. I first learned about this method from IDS's blog to give credit where credits due!

Definitely I need to digest your code further, but I had one question on the theory being followed:-

Maybe I'm interpreting it incorrectly but in solving for the neutral axis depth at the serviceability limit state for determining the value of I_cracked, you seem to do this based on 'areas' of the shapes based on this comment in the code:-

# using the bisection method step the NA
# down until Marea above = Marea below

But shouldn't you determine the neutral axis depth based on an assumed strain profile and work out forces and hence ultimately use force equilibrium (under a given axial and moment) to solve for the neutral axis depth. Assume a given strain under the proportion of moment and axial load and assume a neutral axis depth, then work out bar/concrete forces and then use force/moment equilibrium to iterate for the neutral axis depth that results in force equilibrium. Centroid of the resultant force on the concrete won't be the centroid of the resulting shape you have determined, as strain varies linearly from the neutral axis depth to the point furthest from the neutral axis on the compression side (triangular stress block at SLS usually assumed for example). Then you work out the second moment of areas of bars, concrete and determine the I_cracked based on this SLS neutral axis depth based on strain. Maybe I'm confused though and you are in fact doing this but in a way that's not apparent in reviewing the code (at least to me because python is a bit foreign to me, and well its Sunday after all!).

Many thanks for sharing!

 

[Celt83]

Agent666:

yeah bisection method can be pretty slow sometimes. It worked ok here since the bounds are pretty well defined and linear.

So I'm working on the assumption right now that the angle of the neutral axis is known and it is what is being entered for the loading condition. Everything I've read in my research to this point has the cracked neutral axis calculated with sum of moments of the transformed areas about the neutral axis = 0. The process your describing sounds more like what I've read as the effective moment of inertia at a service load level which you can back determine knowing the Moment-curvature relationship.

Admittedly all the info I've had available to me for research describes the Icracked calculation for a beam bending about it's strong axis. I always interpreted it like calculating Z for steel, the stresses have increased over the whole cross section to just before the point of being plastic. So I wouldn't be surprised if I'm off base here and if I am would appreciate a gently/hard nudge in the right direction to some better research material .

Edit: so I realized I keep saying the neutral axis when what I really mean is the plastic neutral axis. So my script assumes you already know the orientation of the plastic neutral axis and it then determines the depth and associated transformed moment of inertia about the plastic neutral axis.

Open Source Structural Applications:

https://github.com/buddyd16/Structural-Engineering

 

[IDS]

It's not clear to me whether Kootk is looking for elastic section properties (ignoring concrete in tension), or ULS. Also I don't know if the section properties are what he actually needs, or if he wants them to do a stress or strength analysis.

If elastic analysis, denial or Celt83's work should do it.

For a ULS analysis my spreadsheet will do the design, and will return the section properties, based on a rectangular stress block. I tried it out with a section similar to that in the OP. See output below, and spreadsheet attached.

Doug Jenkins
Interactive Design Services

http://newtonexcelbach.wordpress.com/

 

[Agent666]

Effective moment of inertia (the value you might actually use in an analysis for assessment of deflections) simply scales/adds in another component on top of the I_cracked value to address tension stiffening effects. This accounts for the bits between the cracks stiffening things up as they are not fully cracked through to the neutral axis depth.

In a cracked section the neutral axis is at the depth of zero strain obviously, this is true at the ultimate and serviceability limit states (plane sections remain plane and all that good stuff). Once there is an axial load I believe however that the following statement is not true:-

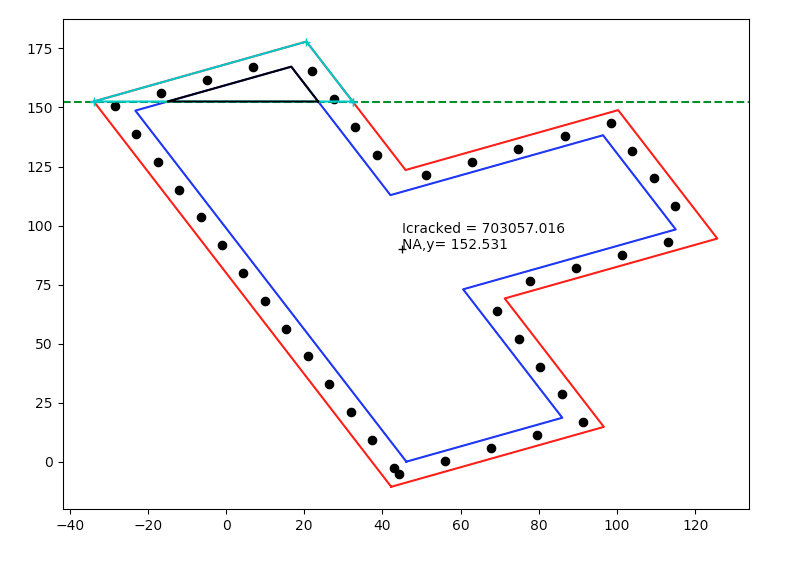
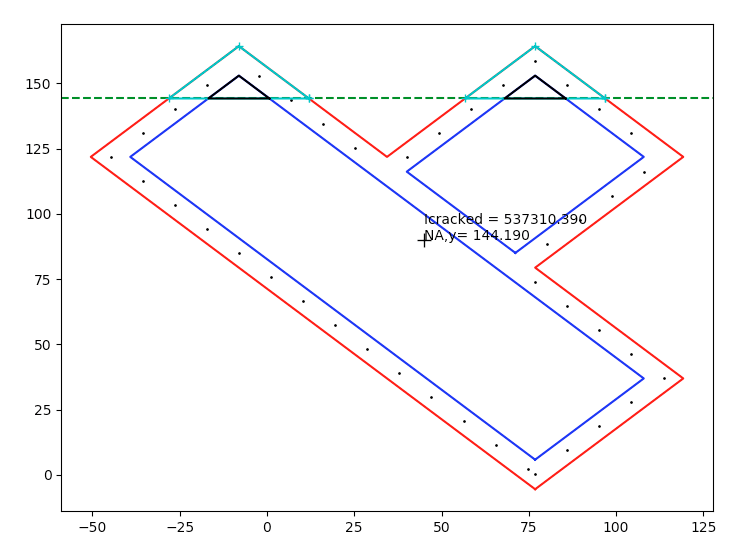
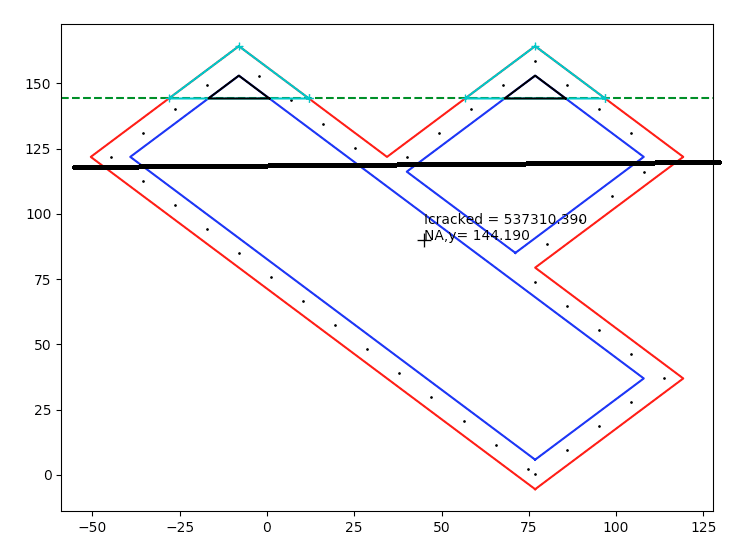
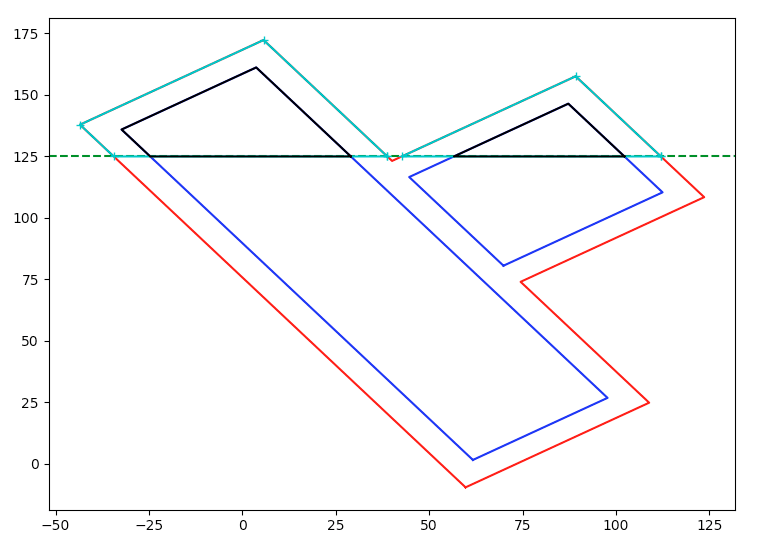
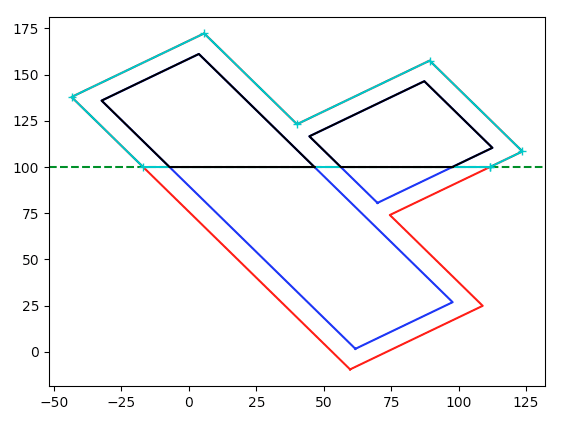
cracked neutral axis calculated with sum of moments of the transformed areas about the neutral axis = 0.

This is is true for pure bending. For bending there is internal equilibrium (so the 1st moment of area approach works), with an external axial load this load needs to be factored into the analysis somehow.

I'd assumed from the original question that it was some sort of building core carrying flexure and axial loads, so axial would need to be considered (though Kootk can weigh in on that).

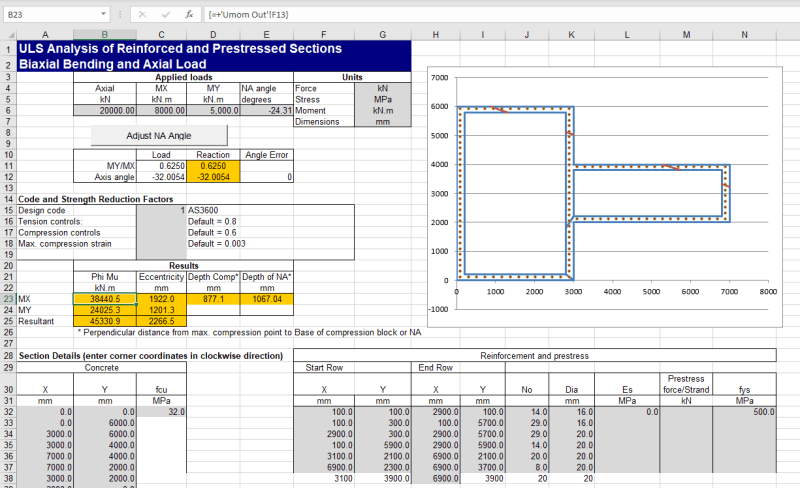
Therefore an alternative approach is to recognise that the reinforcement and concrete stress is linearly related to the distance from the neutral axis. Then work using force or moment equilibrium to solve for the NA depth including the axial load. For a simple beam and a triangular stress block this means the centroid of the concrete force is simply 1/3 x NA depth down from the extreme compression fibre. However for highly irregular sections like your test sections its not so simple obviously assuming you have an axial load and irregular geometry!

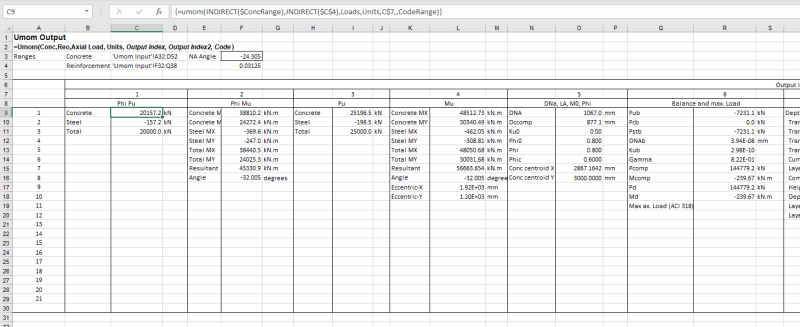
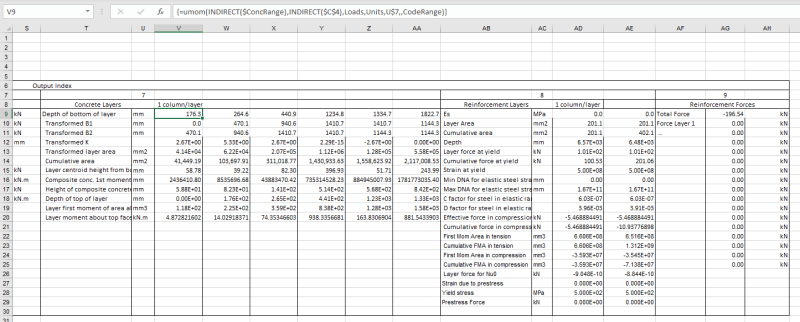
But if you already have it sliced into polygons and you know the strain because you know the depth, you can work out the stresses and hence integrate numerically the 'volume' of stress over the depth of the slice and width (assuming in most cases its broken down into a shape with linear edges) to find the total force and the centroid of this force in each layer (even using something as simple a simpsons rule can work here).

In VBA at least this was starting to get real messy as I was actually doing it at the ULS and looking at using the Eurocode parabolic compression block, so the stress varied parabolically over the depth of a given slice. I had all the numberical integrate bit working using the Tanh-Sinh quadrature routine posted on IDS's website, but it was the slicing bit I was having issues with under a few cases as I never thought of having +ve concrete -ve void approach like you are doing (I was doing something completely different that in hindsight looks like I was way off on a tangent), so I put it on hold a while back and never came back to it!

FYI, an excerpt from my old university notes (attached if its any help) say to either find the neutral axis position by
[ol 1]
[li]1st moment of areas (which is ok if there is no axial load) or (Your approach, and my notes state this verbatim)[/li]
[li]trial and error in balancing forces[/li]
[/ol]

I've always gone down the trial and error balancing forces approach myself and completely read over the 'for force equilibrium the sum of transformed area about the neutral axis = 0' alternative which is why I questioned things!


EDIT - Celt83 I see your edit regarding plastic neutral axis as I was typing this up, I am referring to the neutral axis at serviceability. The term plastic neutral axis and Icr at ULS doesnt have much meaning to me, maybe its in codes other than mine and has some practical design use.
I think at serviceability, you are correctly working it out if there was no axial load.