Frank Richter
Materials
Dear Community,
I observe an unexpected behavior in my simulations and I'd need an advice.
My simulations model the contact of two bars with different cross-sectional areas when exposed to pulse loading.
I have modelled this process in Abaqus/Explicit as a two-dimensional simulation. The investigation was conveniently done as a parametric study, defining the lateral dimension of the second bar as parameter. Both bars are slim (length 2 m, diameter 2 cm) and elastic.
Elements:
CAX4R is the only axisymmetric solid element available in Abaqus/Explicit with four nodes
CPE4R is the only plane strain solid element available in Abaqus/Explicit with four nodes
CPS4R is the only plane stress solid element available in Abaqus/Explicit with four nodes
Contact is defined as CONTACT PAIR with the penalty constraint. Surfaces are element-based. Abaqus was run in double precision.
The identical incident pulse is fed into all simulations. All data of this pulse have the same sign.
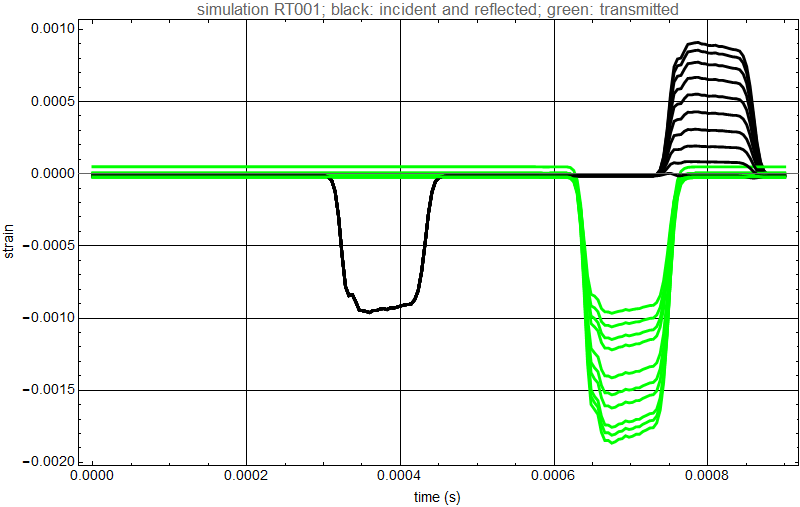
Attached are graphs from the parametric study using axisymmetric elements. A superposition of all simulations from one of the parametric studies is shown, comprising three strain signals each: the incident pulse (they all superpose identically as the same pulse is fed in), the reflected pulse and the transmitted pulse. The cross-sectional area of the second bar is modified from simulation to simulation. Plotted is the total vertical range and an enlargement.
The reflected and transmitted strain signal are recorded at different times as the distance from this virtual strain gage to the interface is different for the two bars.
Observation for CAX4R elements:
the strain traces do not begin at zero strain, even the sign is not consistent.
The strain traces in equivalent graphs from plain strain and plane stress elements are very close to zero.
The elements do not distort excessively (no friction, Poisson's ratio = zero, second bar is free to move axially). Hence, hourglassing should not be the cause.
Kindly advise me.
Thank you for generously sharing your expertise,
Frank Richter
I observe an unexpected behavior in my simulations and I'd need an advice.
My simulations model the contact of two bars with different cross-sectional areas when exposed to pulse loading.
I have modelled this process in Abaqus/Explicit as a two-dimensional simulation. The investigation was conveniently done as a parametric study, defining the lateral dimension of the second bar as parameter. Both bars are slim (length 2 m, diameter 2 cm) and elastic.
Elements:
CAX4R is the only axisymmetric solid element available in Abaqus/Explicit with four nodes
CPE4R is the only plane strain solid element available in Abaqus/Explicit with four nodes
CPS4R is the only plane stress solid element available in Abaqus/Explicit with four nodes
Contact is defined as CONTACT PAIR with the penalty constraint. Surfaces are element-based. Abaqus was run in double precision.
The identical incident pulse is fed into all simulations. All data of this pulse have the same sign.
Attached are graphs from the parametric study using axisymmetric elements. A superposition of all simulations from one of the parametric studies is shown, comprising three strain signals each: the incident pulse (they all superpose identically as the same pulse is fed in), the reflected pulse and the transmitted pulse. The cross-sectional area of the second bar is modified from simulation to simulation. Plotted is the total vertical range and an enlargement.
The reflected and transmitted strain signal are recorded at different times as the distance from this virtual strain gage to the interface is different for the two bars.
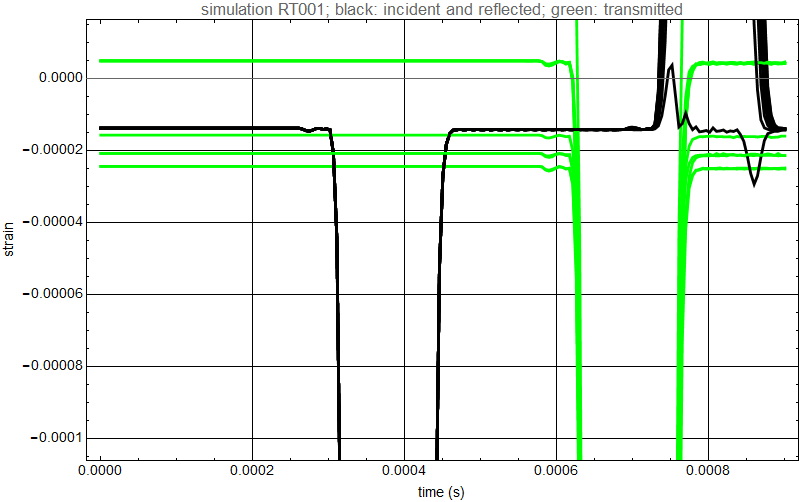
Observation for CAX4R elements:
the strain traces do not begin at zero strain, even the sign is not consistent.
The strain traces in equivalent graphs from plain strain and plane stress elements are very close to zero.
The elements do not distort excessively (no friction, Poisson's ratio = zero, second bar is free to move axially). Hence, hourglassing should not be the cause.
Kindly advise me.
Thank you for generously sharing your expertise,
Frank Richter


