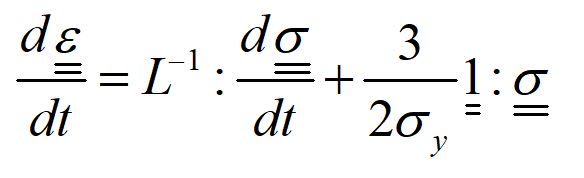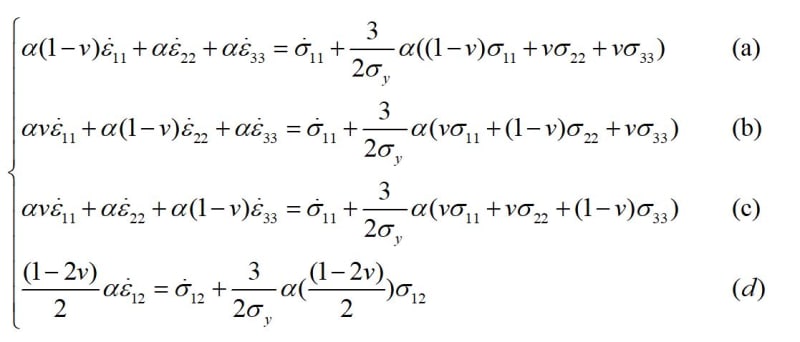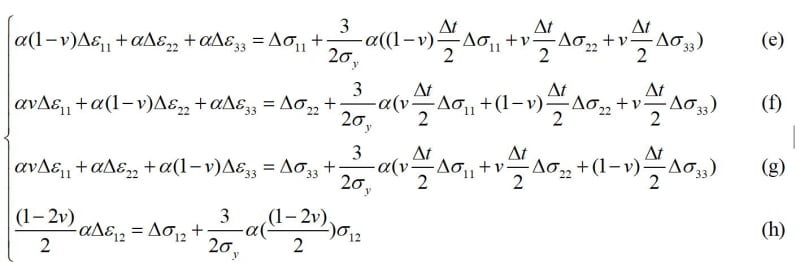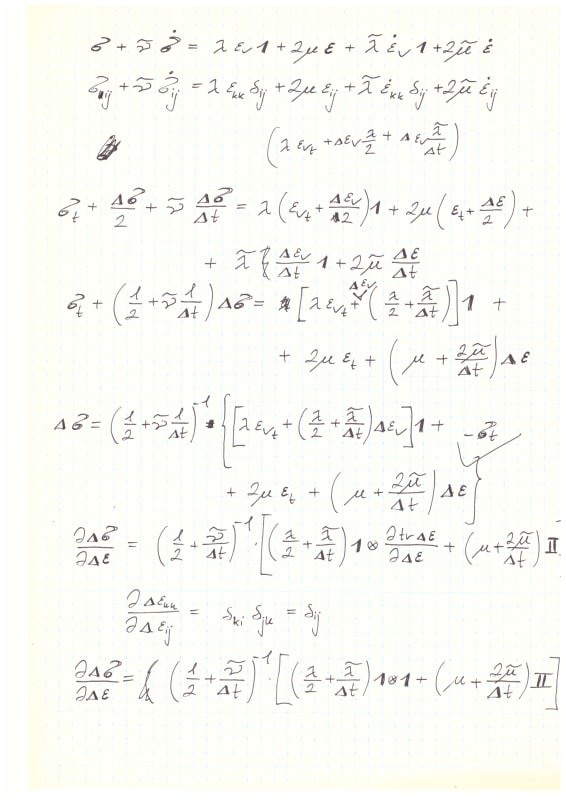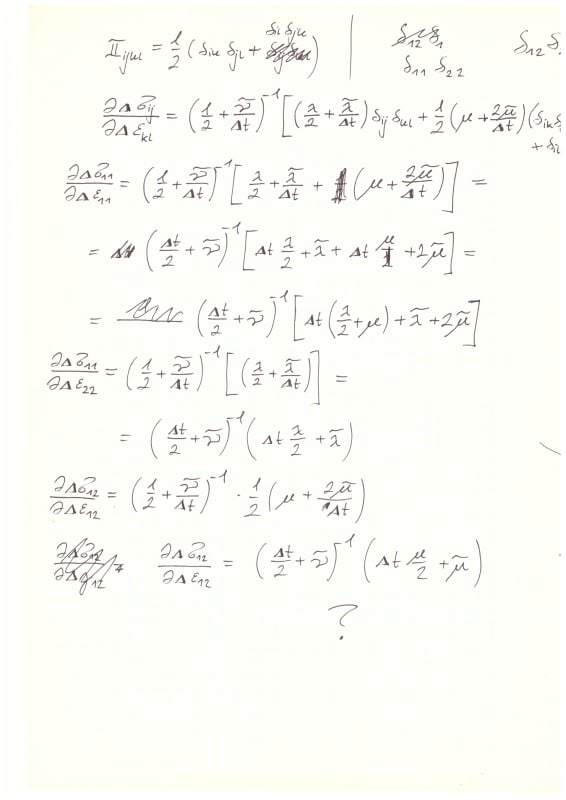Jacobian matrix DDSDDE- UMAT 1

[Lemine]

Hello everyone,

Can anyone help me to obtain the tangent matrix of this behavior law (to use in UMAT subroutine) and il would be so thankful?

Thanks in advance

 

[Cyprek]

Hello,

The way I see it there is something wrong with your equation. On the right hand, the double dot product of second order unit tensor and the stress tensor would result in a scalar value (namely the trace of the stress tensor). So I think that the second term on the right side of the equation is lacking a unit tensor "1".

Furthermore, L-1 is probably a fourth order tensor. If you multiply it (double dot product) with the time derivative of stress (second order tensor) you will get a second order tensor. This way all the terms in yuor equation will be second order tensors.

In order to derive the tangent operator (DDSDDE) you need to replace the differential equation that you posted with a recurrence-update formula. This can be done using the central difference method.

Here is a link to example where this procedure is followed for a more complicated case (standard viscoelastic solid; scroll down to the picture with springs and dashpot):

http://130.149.89.49:2080/v6.10/books/sub/default.htm?startat=ch01s01asb36.html

Using the central difference method you need to obtain an equation for the stress incremenet. Then, you differentiate the stress increment with respect to the strain increment. You will obtain the searched operator this way.

 

[Lemine]

Many thanks to you dear Cyprek for the detailed explanation and for the link.
you have right L-1 is a fourth-order tensor. I would be so thankful if you can verify if this I write is correct.
I multiply the équation above by the fourth-order tensor L (Hooke's law), my problem is 2D so :
I found the equation system (a, b, c, d) below, alpha and nu are constant:

Then I use the example you have sent to me and I obtain the equation system(e,f, g, h):

but how I can obtain the DDSDDE?
Thanks in advance for your help

Best regards

 

[Cyprek]

Hello,

Unfortunatelly, in order to check your derivations I would have to make some derivations myself. I don't want to do that, because I'm a little bit pressed for time. However, I uploaded some derivations which I did in the past for the case discussed in the UMAT tutorial included in Abaqus manual. These derivations might be of some use to you. I prefer to use tensor notation (instead of the index notation).

Note that in your case DDSDDE is a 6x6 matrix. It is symmetric and probably many of its components will be zero. It depends on the specific form of the fourth order tensor L.

Best regards

 

[Lemine]

Thank you very much, dear Cyprek.

Best regards