Bruna_Mara
New member
- Feb 11, 2020
- 5
Hello!
I'm an engineering student and I’m trying to learn about laminate plate buckling with FEM analysis, so I did the finite element model and used the linear bifurcation analysis (linear buckling - LBA), but the results are not as expected, according to the reference article that I was following.
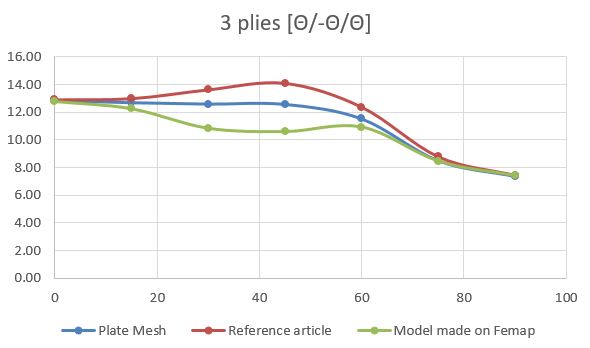
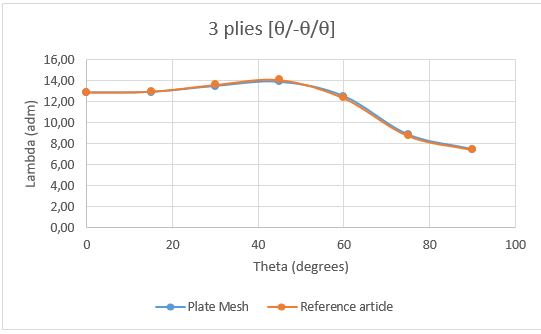
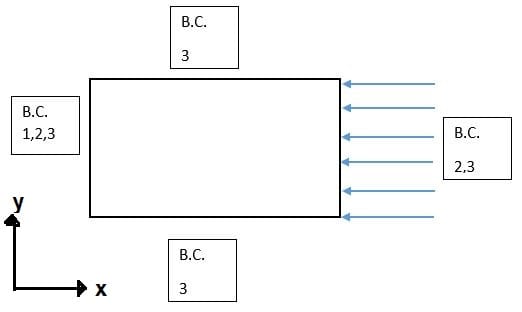
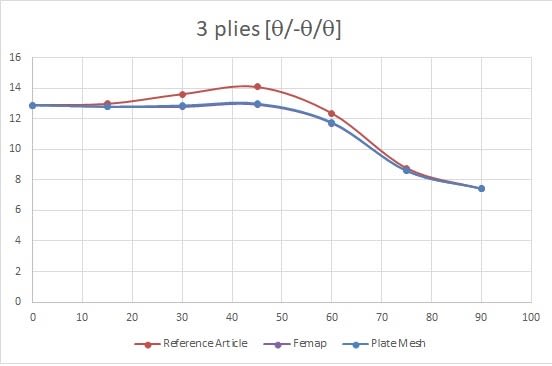
The analysis was made for different fiber angle in each ply [+θ/-θ/+θ], the FEM model is in the link below. The graphic below show the reference results (made by Ritz-method) and the LBA. The critical buckling for +-75 and +-90 are accurate, but the other angles are not. The analysis was performed with Femap and NX Nastran.
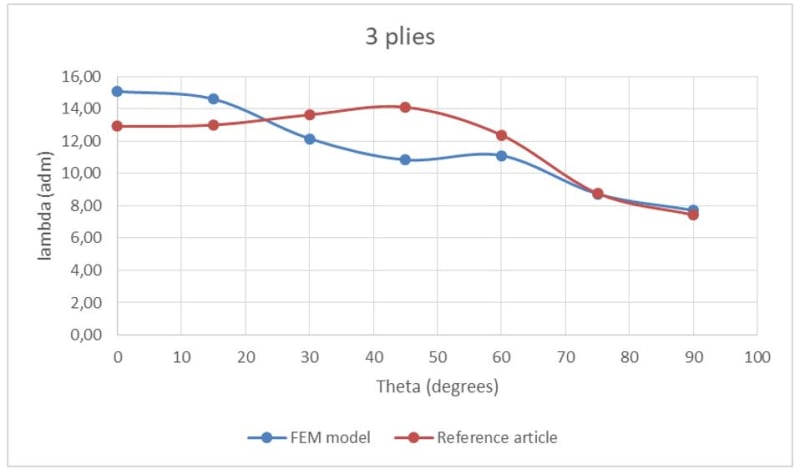
I am trying to identify what could I have done wrong. Does anyone have any idea what I may have done wrong?
The article reference is: BUCKLING STUDIES FOR SIMPLY SUPPORTED SYMMETRICALLY LAMINATED RECTANGULAR PLATES. Yoshihiro Narita. Arthur W. Leissa
Thank you very much!


The model: (the maximum that can be uploaded is 20mb, I had to upload into the drive and share the link.
I'm an engineering student and I’m trying to learn about laminate plate buckling with FEM analysis, so I did the finite element model and used the linear bifurcation analysis (linear buckling - LBA), but the results are not as expected, according to the reference article that I was following.
The analysis was made for different fiber angle in each ply [+θ/-θ/+θ], the FEM model is in the link below. The graphic below show the reference results (made by Ritz-method) and the LBA. The critical buckling for +-75 and +-90 are accurate, but the other angles are not. The analysis was performed with Femap and NX Nastran.

I am trying to identify what could I have done wrong. Does anyone have any idea what I may have done wrong?
The article reference is: BUCKLING STUDIES FOR SIMPLY SUPPORTED SYMMETRICALLY LAMINATED RECTANGULAR PLATES. Yoshihiro Narita. Arthur W. Leissa
Thank you very much!


The model: (the maximum that can be uploaded is 20mb, I had to upload into the drive and share the link.