Blackstar123
Civil/Environmental
I'm reviewing the design calculation of anchoring to concrete checks, submitted by another design firm.
The designer has calculated the pull out capacity of L bolts using the following formula, which is contrary to the one given in Chapter 17.
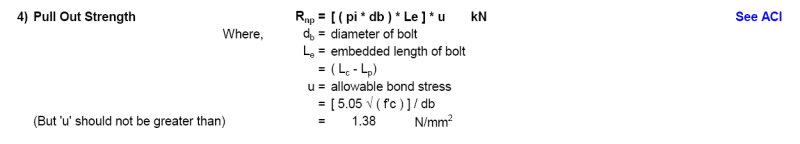
I am having difficulty finding out the reference of the above formula in regards with "anchor bolts". As I understand the pull out strength of anchor bolt is governed by the bearing on the L part only, and any bond stress developed due to friction is ignored.
Before I asked the designer to furnish the said reference, I want to ask if someone here could point me in the right direction.
The designer has calculated the pull out capacity of L bolts using the following formula, which is contrary to the one given in Chapter 17.
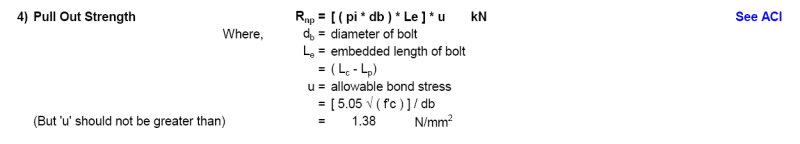
I am having difficulty finding out the reference of the above formula in regards with "anchor bolts". As I understand the pull out strength of anchor bolt is governed by the bearing on the L part only, and any bond stress developed due to friction is ignored.
Before I asked the designer to furnish the said reference, I want to ask if someone here could point me in the right direction.

![[smile] [smile] [smile]](/data/assets/smilies/smile.gif)

