The figure (attached) shows the arm of a lift in the particular position in which while the adjustment tie rod CB is horizontal, it also happens that the section of the lifting cable DE is horizontal. With the measurement dimensions and with the mass M = 500 kg to be lifted, the loads on the hinges A, B, C and on the pin D of the pulley are calculated; also choose the profile and dimensions of the arm AD.
exercise 2 construction solution: Make a construction drawing of the connection between the arm and the pulley (D) and between the arm and the hydraulic piston (B)
My hypothetical solution is the following:
equilibrium condition of the point of material of mass M, or T = Mg directed upwards, applied to the center of gravity. Then considering the pulley for the 3rd principle of dynamics there is tension of the wire acting in the downward direction equal to T.
To derive the reactions of the hinges I thought of calculating the moment with respect to the intersection of the points A and C (bottom point) in order to eliminate 3 reactions out of 4 in the hinges A and C. What does not make sense to me is that I cannot calculate the distance between C and D for reactions in D. I hope that someone can give me a hand in the resolution.
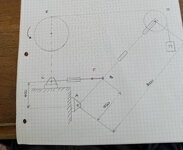
exercise 2 construction solution: Make a construction drawing of the connection between the arm and the pulley (D) and between the arm and the hydraulic piston (B)
My hypothetical solution is the following:
equilibrium condition of the point of material of mass M, or T = Mg directed upwards, applied to the center of gravity. Then considering the pulley for the 3rd principle of dynamics there is tension of the wire acting in the downward direction equal to T.
To derive the reactions of the hinges I thought of calculating the moment with respect to the intersection of the points A and C (bottom point) in order to eliminate 3 reactions out of 4 in the hinges A and C. What does not make sense to me is that I cannot calculate the distance between C and D for reactions in D. I hope that someone can give me a hand in the resolution.

