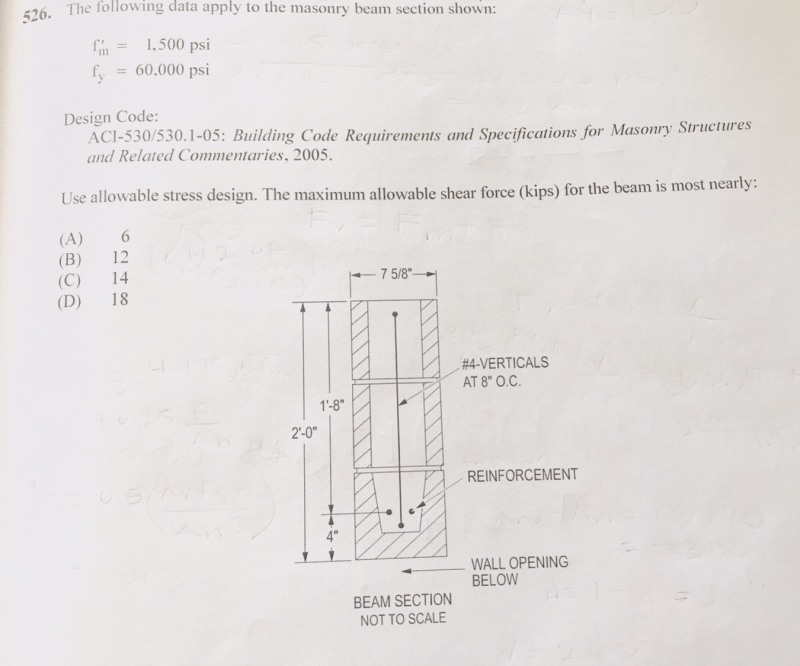
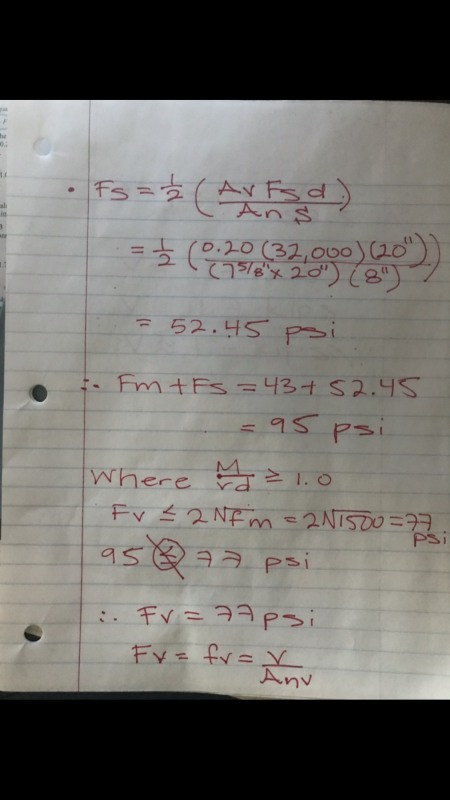Hi everyone. I was wondering if anyone knows what is considered the "net shear area" in a masonry beam. I went through the current masonry code and searched online and it seems to be equal to An which is the cross sectional area. In other words Anv=An. however when im calculating the max allowable shear force (ASD), I get a big number in kips and I feel like maybe it's because these areas are actually different. I tried playing with different possibilities for Anv but I still won't get the right answer. any comment would be very helpful for me if anyone has a clue thank you. below is problem statement (from ncees practice workbook , answer is 12 kips)and then I put down pictures of my calculations
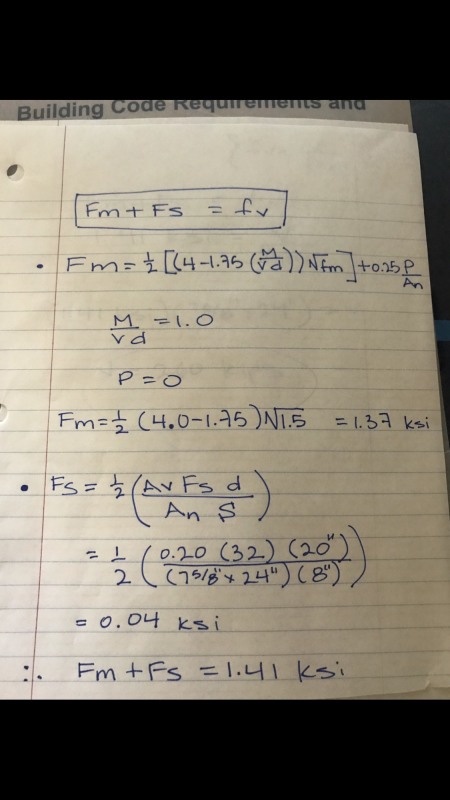
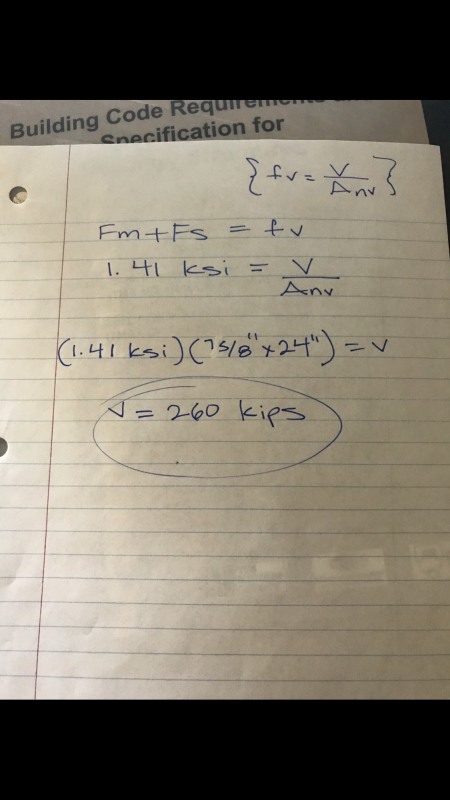

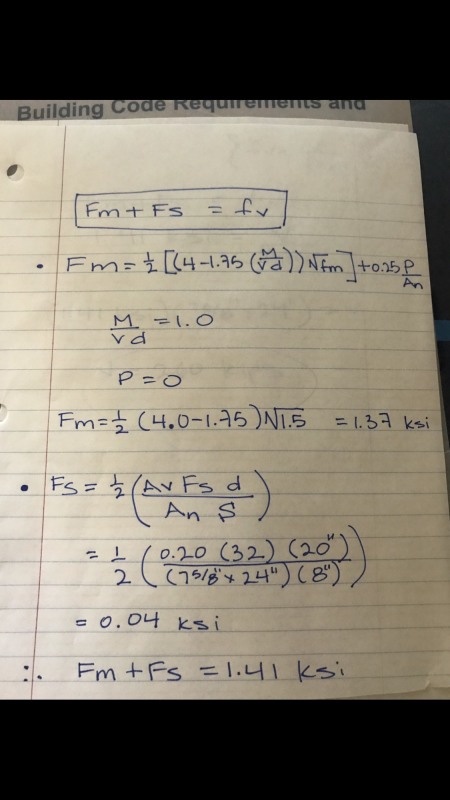
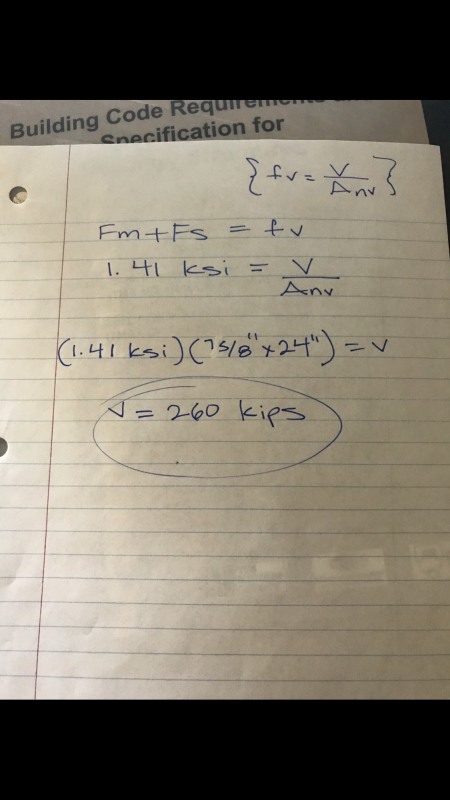

![[smile] [smile] [smile]](/data/assets/smilies/smile.gif)