maximum vs average shear stress in shear pins

[JanEngineer]

Hi all,

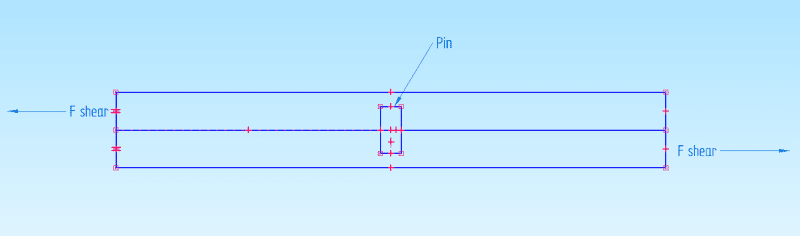
Currently I am doing some calculations which involve shear forces in pins (retrieved from FEA). The maximum shear factor for a round pin would be 4/3. However I am wondering if this also applies for pins with in plane shear. The pins are forced into a hole and connect two flanges. There is no clearance between the pin and the hole.

The maximum shear factor applies to the axial shear stress. However, because moment equilibrium this would also be the shear stress in transverse direction. In this case however I don't see the axial shear stress to be an issue. Is it therefore okay to use the average shear stress instead?

Could anyone offer some clarification? Preferably I would like to have an answer that can point to a norm or some sort of authority such that I can clarify why I don't use the shear factor.

Thanks in advance!

 

[klaus.]

could you make a little sketch ?

 

[JanEngineer]

basically my question is just that if I want to calculate the shear stress in the pin should I use shear_stress=F/A or k*F/A, where k is the shear factor of 4/3 in this case.

This shear factor is based the shear in axial direction. Example and explanation here:

https://wp.optics.arizona.edu/optomech/wp-content/uploads/sites/53/2016/10/OPTI_222_W10.pdf

I'm just wondering if this is also the case for in plane shear because the pin does not really bend in this case.

 

[klaus.]

in my opinion you can use : shear_stress = F/A
in that case

 

[JanEngineer]

Thanks for your reply. Is there any way to justify this? Would you include this shear factor if it where a bolt with clearance? My colleagues always use this shear factor "k". A third official party will have to verify our calculations.

 

[kingnero]

4/3 is for a circle, this looks like a rectangular cross section then k = 1.5 not 4/3

 

[JanEngineer]

Sorry I didn't clarify enough. The picture drawn is a cross section. In reality the pin is a circle. So you think a k value should be used in this case?

 

[DrZoidberWoop]

I would use a simple safety factor on the pin and be sure to include the St. Venant's principle for the stress concentration in the plates. That would be my rough approach. Sophisticated FEA with contact forces enabled will be more precise and you can decrease your safety factor according to your model's reliability.

 

[JStephen]

The shear distribution used for beams is based on a "long" section and is valid away from supports, and would not be applicable to a shear pin.
Usually, in a situation like that, the code that specifies the allowable stress would also specify how it is determined, whether P/A or what.

 

[rb1957]

how about using the allowable (load) from a similar bolt ?

another day in paradise, or is paradise one day closer ?

 

[canwesteng]

If you're concerned about combining flexural stresses and shear stresses, use either von mises or principal stress formulas. If you just want to look at longitudinal shear stress for some reason, you need to include the k factor, because the transverse shear and longitudinal shear are equal. Unless you are laminating the pin I'm not sure what the purposes of this is though.

 

[JanEngineer]

It is a case of transverse shear only. There are bolts which take the longitudinal loads and shear pins which take the shear load (free to move in axial direction). I know the transverse and longitudinal shear are equal. I am just wondering if the distribution is really correct in this kind of case. The longitudinal shear is based on bending of a "beam" in which case the longitudinal stresses are introduced (see my first link). If the shear acts in a single plane then perhaps the shear distribution is just equal along its surface area? Also when I look at online pin calculations they always calculate the average shear. I am still searching for a norm based calculation. It is very difficult to find any information on this online.

I notice not everyone is agreeing at the moment on whether or not to include the k factor. I do greatly appreciate all your answers.

 

[robyengIT]

As far as I understand (may be I am too rough) your situation is similar to a cutting machine. Half of the pin is locked by a vice (lower flange) and the other half is cut by the blade (upper flange). For me there is no "k" factor

 

[canwesteng]

Go back to your continuum mechanics textbook. If you draw a small element at the edge of the section, how can shear be resisted at the free edge? Therefore shear still needs to go from zero at the edge to a maximum value in the middle. But the plastification of the pin complicates things. Refer to an applicable code in your region for a formula for this. For example, CSA S16 allows average shear stress to be used, and 0.66F.y instead of 0.57F.y as your shear stress resistance because of this. On a purely elastic level I believe k applies and if I had no code reference to use for additional capacity that is what I would use.

 

[dhengr]

JanEngineer:
Look in any number of good Strength of Materials or Theory of Elasticity textbooks, the 4/3 and 3/2 factors are for round bars and rectangular bars respectively, and are the max. shear stresses in the bars, at the neutral axis, associated with bending moments and normal stresses, when the bars are acting as spanning beams. The shear stress varies across the depth of the section. These are max. shear stress magnitudes, (4/3)(V/A) and (3/2)(V/A), at the neutral axis, for round and rectangular bars respectively, and we often express/calculate/plot them as VQ/bI. Your condition is a round pin being cleaved, in shear, at a faying surface. And, the shear stress is typically expressed simply as F/A in psi. The “F” in your sketch could be the horiz. shear flow summation, over some length, in a bending bar/beam at any height away from the neutral axis, or it could be an actual pair of shearing forces pulling in opposite directions along the axis of the beam, but they both produce essentially a cleaving shearing action on the pin/rivet/bolt. Then, you could have combined stress conditions, maybe a torsional loading which would induce a cleaving shear load/stress, across the pin, perpendicular to the first shear above. And, you might have a shear and bearing stress or pin bending stress in the pin causing a higher combined stress. If the pin was in a tight pressed-fit condition this would produce some additional combined stresses. This actually can become a fairly complex problem, so don’t over complicate it at the outset.