feensm
Mechanical
- Apr 3, 2019
- 2
Hello All,
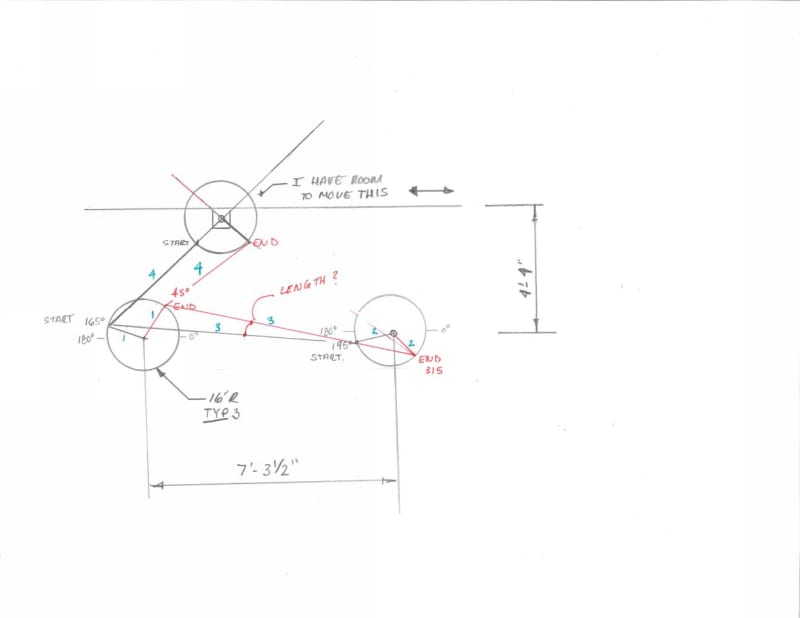
I am trying to design a linkage system to close and open a bypass plate that weights roughly 200lb. I have two fixed points of rotation and the arms are the same length. I don't understand why the bar between them is not the same length at start and end point of the rotation when they are complementary angles. Can someone explain what I am not thinking about. This lever will be operated from the deck above
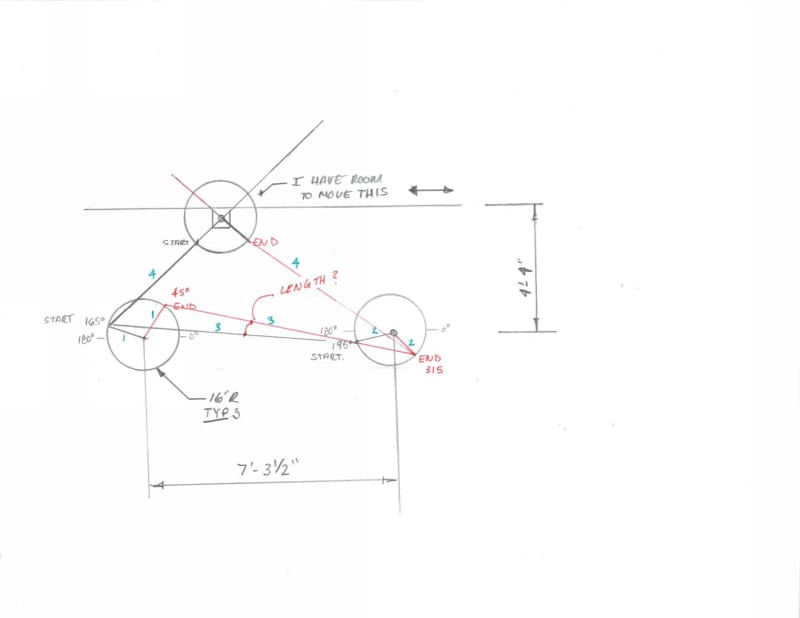
This is myh first time ever designing something like this as you can tell I'm sure. I am stuck and don't know where to go.
Thanks
I appreciate the help
I am trying to design a linkage system to close and open a bypass plate that weights roughly 200lb. I have two fixed points of rotation and the arms are the same length. I don't understand why the bar between them is not the same length at start and end point of the rotation when they are complementary angles. Can someone explain what I am not thinking about. This lever will be operated from the deck above

This is myh first time ever designing something like this as you can tell I'm sure. I am stuck and don't know where to go.
Thanks
I appreciate the help