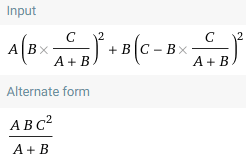StrEng007
Structural
- Aug 22, 2014
- 512
For composite shapes, I've typically calculated Ix by means of a parallel axis (located at the neutral axis for the overall shape). For the image below, Ix would be:
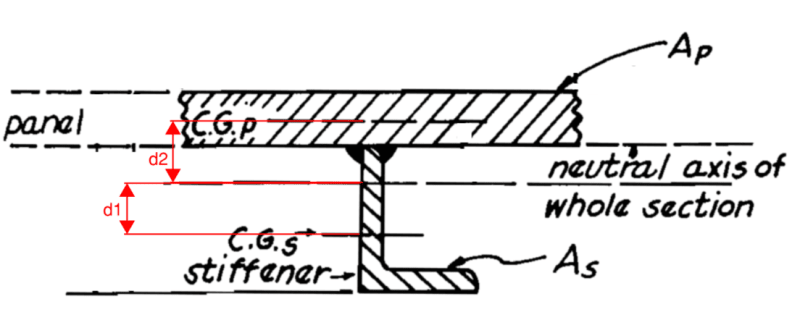
Ix = [Is + As(d1)²] + [Ip + Ap(d2)²]
Where:
Is = moment of inertia for the stiffener (angle)
As= area of stiffener (angle)
d1 = distance from centroid of the stiffener to the centroid of the composite shape
Ip = moment of inertia for the panel (plate)
Ap= area of the panel (plate)
d2 = distance from centroid of the panel to the centroid of the composite shape
To use this approach, you much first calculate the location of the Neutral Axis.
However, I came across this formula that calculates the same Ix.
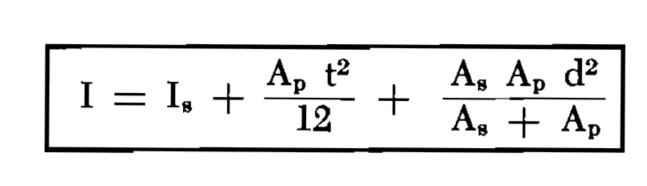
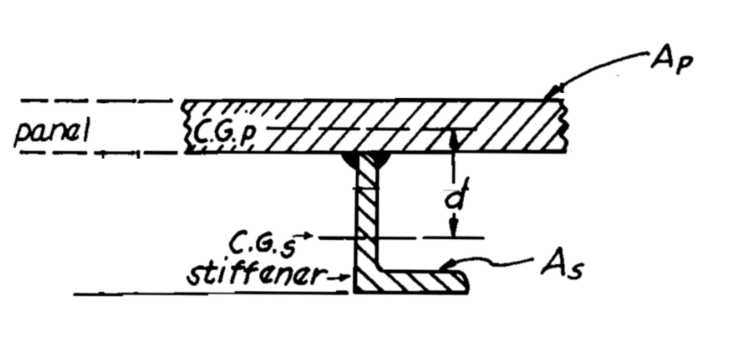
The first two values are the moment of inertia of the stiffener and plate, respectively. The third values provides a short cut to using the parallel axis (ie, you don't need to calculate the Neutral Axis of the cross section). Is there a particular name for this method? It seems like a much quicker way to calculate Ix of a composite shape. I'm trying to find any text that has a more thorough discussion on this.
Note: This method comes from Blodgett's welded structures, section 6.4.

Ix = [Is + As(d1)²] + [Ip + Ap(d2)²]
Where:
Is = moment of inertia for the stiffener (angle)
As= area of stiffener (angle)
d1 = distance from centroid of the stiffener to the centroid of the composite shape
Ip = moment of inertia for the panel (plate)
Ap= area of the panel (plate)
d2 = distance from centroid of the panel to the centroid of the composite shape
To use this approach, you much first calculate the location of the Neutral Axis.
However, I came across this formula that calculates the same Ix.
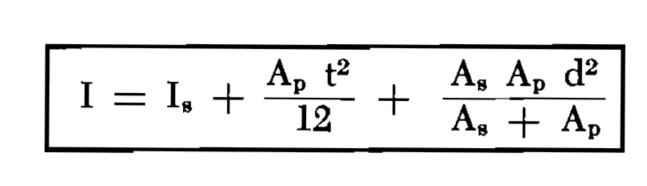

The first two values are the moment of inertia of the stiffener and plate, respectively. The third values provides a short cut to using the parallel axis (ie, you don't need to calculate the Neutral Axis of the cross section). Is there a particular name for this method? It seems like a much quicker way to calculate Ix of a composite shape. I'm trying to find any text that has a more thorough discussion on this.
Note: This method comes from Blodgett's welded structures, section 6.4.