Moment of inertia using Coordinate system

[ArunKumar Bala]

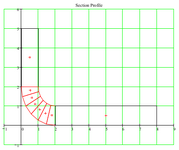
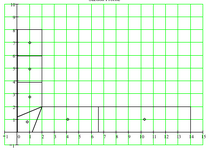
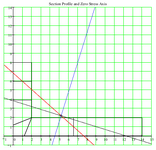
Hi all, I am trying generate one spreadsheet program which will give answer for moment of inertia using the inputted coordinates. can any body guides me how can we input the formulas for coordinate systems. I have come across various books like Niu, Megson, Bruhn which all tells for particular shapes only with predetermined formulas but i am not able to see for inertia using coordinate systems.

Note : Coordinate systems will generate various complex shapes which is used in aerospace industry like Z, C, I section with complex radius in 2D.

 

[SWComposites]

break each section down into a set of rectangles, then use the equations in various texts. or derive those equations from basic section properties principles.

 

[Stress_Eng]

I've used a number of approaches to calculate section properties for an irregular cross-sectional shape. With a set of profile coordinate, most of the time I use a curve fitting method (spline functions in Mathcad), so a function can be used to describe outer / inner profiles. Having functions such as y_outer(x) and y_inner(x), the standard integration methods usually do the trick! For a spreadsheet approach, you could look at using a Hero's Formula method. The profiles shown are examples, where each sub-section is divided into 4 triangles. The 2nd and 3rd examples enable axial, bending and shear flow calc's to be conducted (at elbow, inscribed circle contact points at outer profile for torsional shear stress). A tabular approach could be conducted.

Hope these examples give some ideas!

 

[LiftDivergence]

I don't think you want to look at Niu, Megson, or Bruhn for this. Instead look in any Strengths of Materials / Mechanics of Materials Textbook, look in the index, and find where they cover topics like "moment of area for composite shapes", "parallel axis theorem" etc.

These methods generally rely on breaking a complex shape down into smaller, simpler approximate pieces, selecting a reference origin and coordinate system, and then using the parallel axis theorem and summation.

 

[rb1957]

I wonder what Abbott Aerospace has to say ? they are usually pretty good with this type of analysis.

One thing to think about is what you want to use the geometry properties for. Do you want an overall perimeter ? Torsion properties ?? The simple stuff (A, I, NA, etc) are all simply done with rectangles or other simple shapes and a simple s/sheet (excel).

How do you want to input the data ? Simple sub-areas are usually easy to determine and to enter. Entering the corner co-ordinates is more complicated but can get you more data (like perimeter).

 

[GregLocock]

Bear in mind that Mohr's circle applies.

 

[WKTaylor]

BRUHN CHAPTER A3
Analysis and Design of Flight Vehicle Structures - Chapter A3: PROPERTIES OF SECTIONS - CENTROIDS MOMENTS OF INERTIA ETC.

Also... my company and many proprietary stress analysis manuals to 'deep-dive' into section properties.

Also... as a time savings device, my company's stress weenies have access to many digital stress analysis tools... including making 2D CAD drawing of section profiles... which are then use by a specialize program to generate everything there is to know about that section... IE: area, centroids, mass, axis, moments of inertias, etc for various type materials. They need the tool for beams, spars, longerons, forgings, etc... where section-properties are constantly changing along the section.

I think there are specialty software vendors offering stress analysis tools... such as DAR Corp, Abbottaerospce.com.. etc.

 

[Celt83]

Review Line integrals and parametric equations.

Using those mathematical tools you can solve general functions for a line defined by two points, bezier curves, or true curves using the general integral definitions for section properties.

Once you have the general formula defined for a single element you can use those to generate full closed boundaries for sections.

Section properties for Torsion and shear areas are more complicated and typically solved through finite element methods.