Pavan Kumar
Chemical
- Aug 27, 2019
- 397
Hi All,
I was able to perform pressure drop calculations for develop the system curve with two dissimilar pump using the guidance provided in the below thread. The pump and system curves are pasted below for your reference. I can post the excel calculation spreadsheet also if needed.
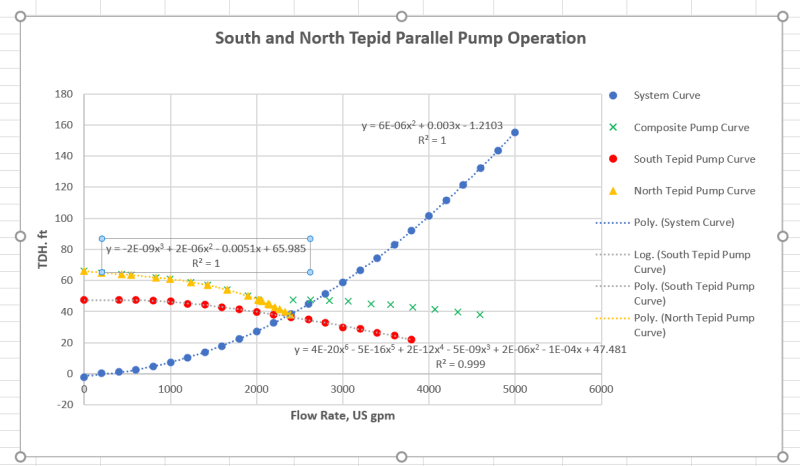
Since I was not able to get the required flow with pumping in parallel, I worked on the option to raise the RPM of the current motor from 1200 to 1800 RPM. The motor HP has increased from 30 HP to 100 HP. We are still checking the feasibility of this option. We are going to use VFD to adjust the RPM as required. I have the Load Performance Curve for the motor (see attached). I want to know the power factor and motor efficiency to calculate the power input required to calculate the electrical power cost / year. My question how do I determine at what percent of the rated output power I am operating my motor. The data I have is based on my pump pressure drop calculations is the Flow rate, head and pump efficiency at the duty point. As you can see in the Load Performance curve the while the motor efficiency more or less remains same as the load decreased the power factor gradually reduces. I want to use the power factor and motor efficiency at the load I am operating at.
Thanks and Regards,
Pavan Kumar
I was able to perform pressure drop calculations for develop the system curve with two dissimilar pump using the guidance provided in the below thread. The pump and system curves are pasted below for your reference. I can post the excel calculation spreadsheet also if needed.

Since I was not able to get the required flow with pumping in parallel, I worked on the option to raise the RPM of the current motor from 1200 to 1800 RPM. The motor HP has increased from 30 HP to 100 HP. We are still checking the feasibility of this option. We are going to use VFD to adjust the RPM as required. I have the Load Performance Curve for the motor (see attached). I want to know the power factor and motor efficiency to calculate the power input required to calculate the electrical power cost / year. My question how do I determine at what percent of the rated output power I am operating my motor. The data I have is based on my pump pressure drop calculations is the Flow rate, head and pump efficiency at the duty point. As you can see in the Load Performance curve the while the motor efficiency more or less remains same as the load decreased the power factor gradually reduces. I want to use the power factor and motor efficiency at the load I am operating at.
Thanks and Regards,
Pavan Kumar
