Motor starting Voltage drop Equation at Transformer Secondary terminals

[NickParker]

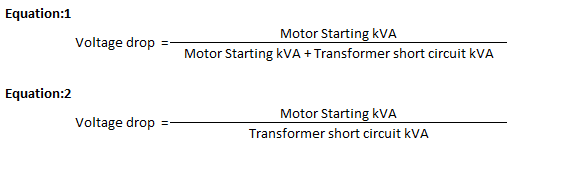
Which is the correct equation below for the Voltage drop while starting of Motor at Transformer secondary terminals. I could understand the Equation (2) as the percent impedance is directly proportional to the transformer kVA rating I could calculate the voltage drop e while Motor starting knowing that percent impedance is the voltage drop when the transformer is loaded to its rating and I could not understand the equation 1.

 

[NickParker]

The Equation(1) is from the book, Industrial Power Systems by Shoaib Khan

 

[dpc]

Both are approximations. Eq 1 should be more accurate. It's related to the voltage divider equation. You're neglecting a lot of things, including the source impedance, and any phase angle difference between the two impedances.

I've never really understood the attraction of using kVA values to calculate fault currents. You have the transformer impedance - must have to know the transformer short circuit kVA. Seems more direct to calculate the approximate motor locked rotor impedance and calculate it the "hard" way. But probably just me.

 

[7anoter4]

For a transformer of 400 kVA 4% zsc and a motor of 160 kW 8*Irat=I lock the first equation error is +45% and the second +68%

 

[NickParker]

The equation 2 is more intuitive to me, however I could not understand the Equation:1, Why should we add the motor Starting kVA in the denominator of equation:1?

In Equation:2, the voltage drop at the transformer terminals is directly proportional to the percent impedance. At rated full load current, the percentage voltage drop at the transformer terminals is equal to the transformer percent impedance value. Therefore for Motor starting purposes, Voltage drop% = (Motor Starting kVA / Transformer Rating kVA) x %Z of transformer (which is Voltage drop % = Motor starting kVA / Transformer Short circuit kVA )

 

[dpc]

Voltage drop is caused by current through impedance, not kVA. The kVA method is simply a means to avoid calculation involving complex impedances. Draw a circuit diagram showing source impedance, transformer impedance and motor locked rotor impedance. Assume transformer and motor locked rotor impedance are purely inductive to simplify. It's not so bad.

 

[HamburgerHelper]

I don't know what equations you are using but you need the thevenin impedance into the grid,too. When you starting a motor, the grid sags. Sometimes a little and sometimes a lot depending on the size of the motor and the strength of the grid.

------------------------------------------------------------------------------------------
If you can't explain it to a six year old, you don't understand it yourself.