jus2sho
Aerospace
- Jul 22, 2009
- 11
Ok, so I have a shaft and a hub that is connected with a solid dowel pin in double shear. I need to calculate the compressive stress in the shaft and in the hub under a torque load. I've found an equation that I believe may be my answer, but can someone please break the equation down for me so I can understand what's actually going on here? Stress is normally calculated by σ = P / A and I understand that T = P*D, but where does the Area fit into the equation below? Please see the attachments for further details. Thanks in advance for any help!
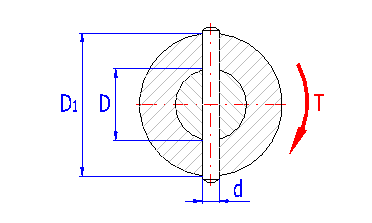
Pressure in Shaft:
- This equation can be rearranged to (6*P)/(d*D). (d*D) is the Area, but how does the multiplier 6 come into play?
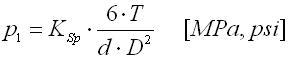
Pressure in Hub:
- Totally lost on this equation. Please explain.
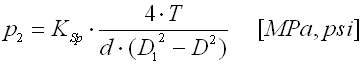
Site For Reference

Pressure in Shaft:
- This equation can be rearranged to (6*P)/(d*D). (d*D) is the Area, but how does the multiplier 6 come into play?
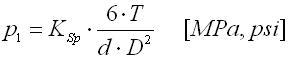
Pressure in Hub:
- Totally lost on this equation. Please explain.
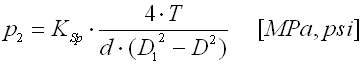
Site For Reference
