Slagathor
Mechanical
- Jan 6, 2002
- 129
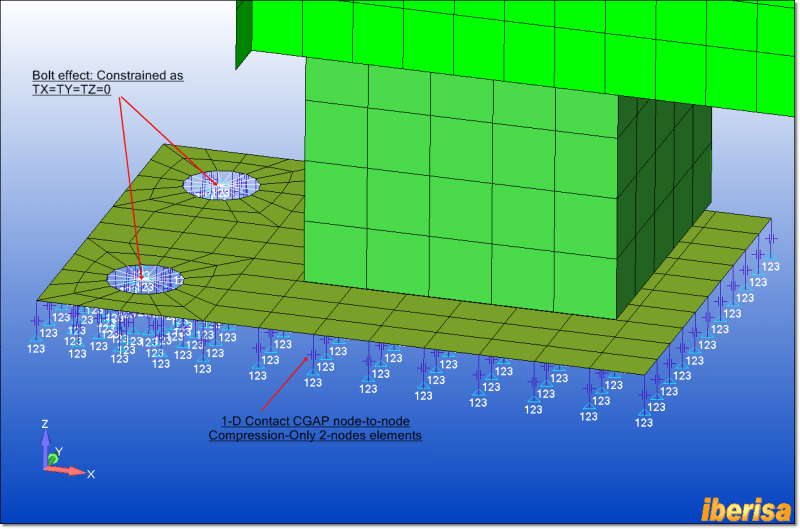
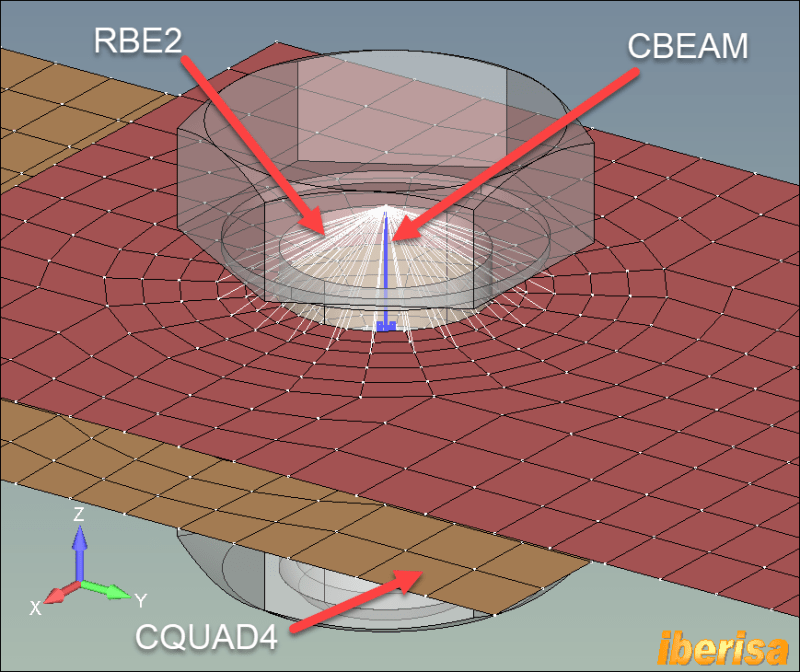
We regularly perform FEA based Modal Analysis on what are essentially cantilevered vertical structures. The bases are bolted joints, and the real world interface between the sole plates and the structure are a can be a source of significant error. If we model as a bonded contact, the calculated stiffness (1st mode frequency) is always too high. It is considerably worse if the base flange of the structure bolted down is thinner. This is because in the real world, a no penetration condition exists. For many points in the contact interface region, for half the motion cycle they can pull away, but for the other half of the cycle they are pressing against the sole plate. It is "half stiff". The region of "half stiffness" is also always changing. It is not fixed. It is also dependent on the magnitude of modal excitation! If the structure is subject to a large exciting force, then more of the interface is half stiff for longer.
In static FEA analysis, a steady state "half stiffness" can be allowed for by using the "No Penetration" boundary condition. But in the FEA programs we have access to (ANSYS, Solidworks/Cosmos, MECWAY), none of them allow for the No Penetration contact in a Modal analysis. I expect this has to do with the underlying nature of FEM Modal analysis, in that you are effectively performing a dynamic analysis, and the boundary conditions for those nodes that are No Pen would change depending on the solution of eigenvalues and the time in the assumed Modal motion cycle. In other words, for each solution, you would have to iterate for the changing boundary conditions in the No Pen area, and it would take for ever to solve, if it ever would converge at all.
Am I off base here, or is there a FEA approach and Code that solves this problem of bolted joints that act differently vs time a load?
Thanks!
In static FEA analysis, a steady state "half stiffness" can be allowed for by using the "No Penetration" boundary condition. But in the FEA programs we have access to (ANSYS, Solidworks/Cosmos, MECWAY), none of them allow for the No Penetration contact in a Modal analysis. I expect this has to do with the underlying nature of FEM Modal analysis, in that you are effectively performing a dynamic analysis, and the boundary conditions for those nodes that are No Pen would change depending on the solution of eigenvalues and the time in the assumed Modal motion cycle. In other words, for each solution, you would have to iterate for the changing boundary conditions in the No Pen area, and it would take for ever to solve, if it ever would converge at all.
Am I off base here, or is there a FEA approach and Code that solves this problem of bolted joints that act differently vs time a load?
Thanks!