Robert_Liang
Mining
- Jun 17, 2019
- 6
I have tried to study Colebrook equation for the relation of open channel slurry flow velocity and solid concentration at certain effective linear wall roughness, hydraulic radius and slope.
From the equation
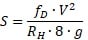[tt] [/tt][tt][/tt](6-6) in Slurry Systems Handbook
It can be derived for velocity as
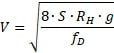
Replace V in Renolds number equation
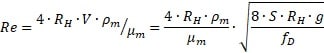[tt][/tt]page 6.31 of Slurry Systems Handbook
Colebrook equation (6-56 in Slurry Systems Handbook) becomes
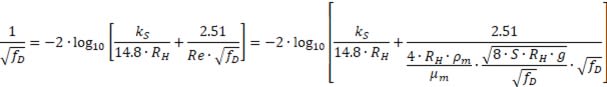[tt] [/tt](6-56) in Slurry Systems Handbook
Thus, Darcy’s friction factor can be derived as
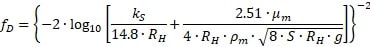
Because μm = f(CVf), the relation of slurry flow velocity and solid concentration can be illustrated below as the open channel wall roughness, hydraulic radius and channel slope are constant.
[ul]
[li] Effective linear roughness kS = 0.013 mm[/li]
[li] Hydraulic radius RH = 0.06536 m[/li]
[li] Slope S=tan(5°)=0.08748866[/li]
[li] Solids density ρ_S=2095 kg⁄m^3[/li]
[li] Liquid density ρ_L=1234 kg⁄m^3[/li]
[li] Slurry density ρ_m=ρ_L+C_V∙(ρ_S-ρ_L )[/li]
[li] Liquid viscosity μL = 0.00167 Pa•s[/li]
[li] Slurry viscosity[/li]
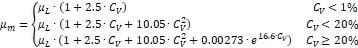
[/ul]
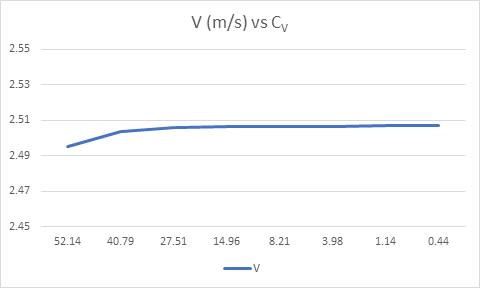
The velocity only changes 0.012 m/s from 2.495 m/s to 2.507 m/s while solid concentration by volume changes from 0.44% to 52.14%. The conclusion is that the slurry flow velocity in an open channel with fixed slope has little relation with solids concentration if it is calculated with Darcy factor and Colebrook equation.
But slurry flow velocity in open channel increases along with solid concentration decreases significantly if it is calculated with the Graf-Acaroglu relation equations.
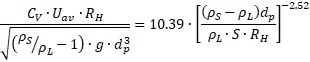[tt][/tt](6-69b) in Slurry Systems Handbook
It can be derived for flow velocity as
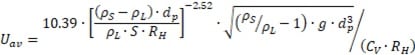
The chart below illustrates the relation of slurry flow velocity and solids concentration by volume, where
• Slope S = tan(4.3°) = 0.07519
• particle size dp = d85 = 0.552 mm
• the rest parameters are the same as those in calculation above
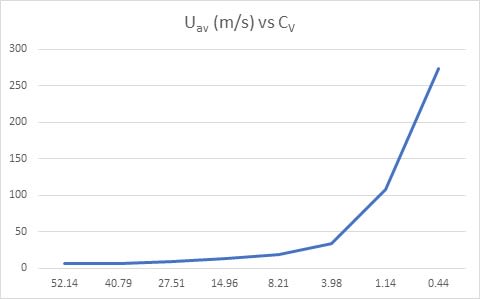
The result is surprisingly different. I doubt the equation of Graf-Acaroglu relation when I see the velocity is calculated above 20 m/s, which is impossible for a gravity flow in open channel. No necessary to mention that the velocity can soar to 273 m/s – close to sonic speed, by the equation. I could not find the exact valid range of CV for Graf-Acaroglu relation in book Slurry Systems Handbook.
The results are so different. I know there were a lot of experiment data of slurry flow to support Graf-Acaroglu relation. Who can verify these two calculations with the data and which method do you support?
Thanks,
Robert Liang
From the equation
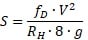
It can be derived for velocity as
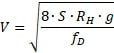
Replace V in Renolds number equation
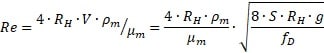
Colebrook equation (6-56 in Slurry Systems Handbook) becomes
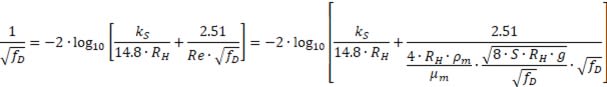
Thus, Darcy’s friction factor can be derived as
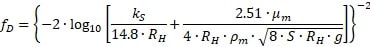
Because μm = f(CVf), the relation of slurry flow velocity and solid concentration can be illustrated below as the open channel wall roughness, hydraulic radius and channel slope are constant.
[ul]
[li] Effective linear roughness kS = 0.013 mm[/li]
[li] Hydraulic radius RH = 0.06536 m[/li]
[li] Slope S=tan(5°)=0.08748866[/li]
[li] Solids density ρ_S=2095 kg⁄m^3[/li]
[li] Liquid density ρ_L=1234 kg⁄m^3[/li]
[li] Slurry density ρ_m=ρ_L+C_V∙(ρ_S-ρ_L )[/li]
[li] Liquid viscosity μL = 0.00167 Pa•s[/li]
[li] Slurry viscosity[/li]
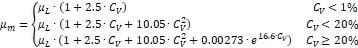
[/ul]
The velocity only changes 0.012 m/s from 2.495 m/s to 2.507 m/s while solid concentration by volume changes from 0.44% to 52.14%. The conclusion is that the slurry flow velocity in an open channel with fixed slope has little relation with solids concentration if it is calculated with Darcy factor and Colebrook equation.
But slurry flow velocity in open channel increases along with solid concentration decreases significantly if it is calculated with the Graf-Acaroglu relation equations.
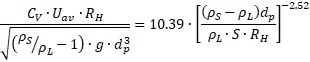
It can be derived for flow velocity as
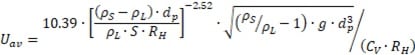
The chart below illustrates the relation of slurry flow velocity and solids concentration by volume, where
• Slope S = tan(4.3°) = 0.07519
• particle size dp = d85 = 0.552 mm
• the rest parameters are the same as those in calculation above
The result is surprisingly different. I doubt the equation of Graf-Acaroglu relation when I see the velocity is calculated above 20 m/s, which is impossible for a gravity flow in open channel. No necessary to mention that the velocity can soar to 273 m/s – close to sonic speed, by the equation. I could not find the exact valid range of CV for Graf-Acaroglu relation in book Slurry Systems Handbook.
The results are so different. I know there were a lot of experiment data of slurry flow to support Graf-Acaroglu relation. Who can verify these two calculations with the data and which method do you support?
Thanks,
Robert Liang
