pyseng
Civil/Environmental
- Nov 9, 2013
- 16
I have recently been interested in using FEA to model and design complex concrete shapes. Through my research, I've found that the Sandwich model, used by SAP2000 and ?Eurocode?, is very logically consistent to me and I would be comfortable using it under the so-called "engineering judgement/rational analysis" provisions of ACI.
However, I just want to make sure I fully understand the methodology before I move forward. I am struggling with one of the concepts presented in the derivation of this method. The figure below is taken from "Optimum Design of Reinforced Concrete Shells and Slabs" by Brondum-Nielsen (which is a primary source reference in the SAP2000 technical note).
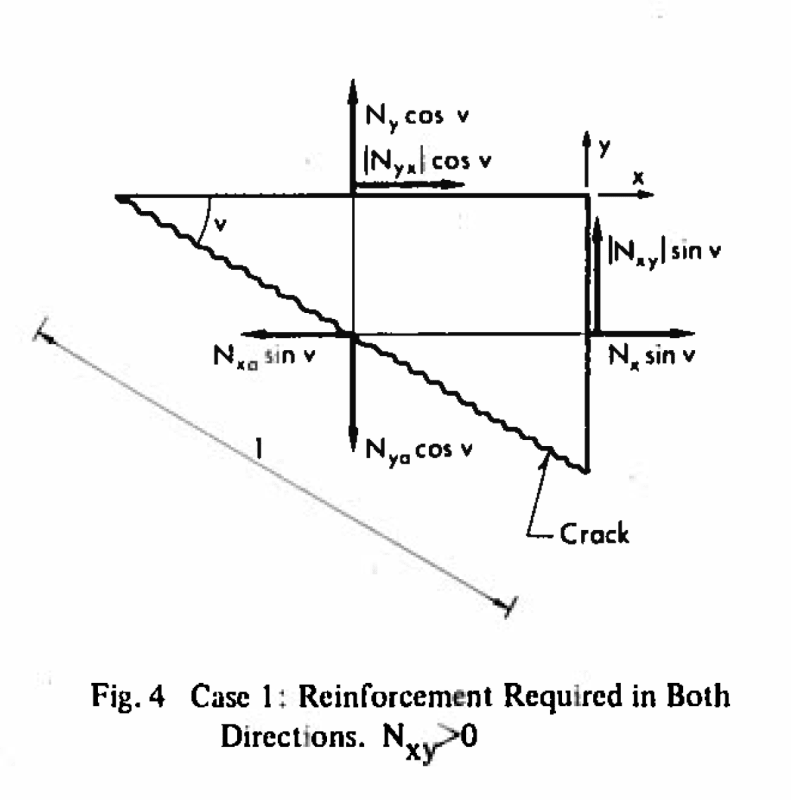
Based on equilibrium, the author derives the equations:
The author then says "If both Nxa and Nya are positive, the necessary reinforcement is proportional to Nxa + Nya. Minimum of reinforcement thus corresponds to v = 45 deg."
Therefore, cot(v) = tan(v) = 1 and the final equations are given as:
Even though the author provides an explanation for taking v = 45 deg, I still just don't understand it. I was hoping that someone with some experience here might be able to offer an alternate explanation. Thank you!
However, I just want to make sure I fully understand the methodology before I move forward. I am struggling with one of the concepts presented in the derivation of this method. The figure below is taken from "Optimum Design of Reinforced Concrete Shells and Slabs" by Brondum-Nielsen (which is a primary source reference in the SAP2000 technical note).

Based on equilibrium, the author derives the equations:
Nxa = Nx + abs(Mxy)*cot(v)
Nya = Ny + abs(Mxy)*tan(v)
The author then says "If both Nxa and Nya are positive, the necessary reinforcement is proportional to Nxa + Nya. Minimum of reinforcement thus corresponds to v = 45 deg."
Therefore, cot(v) = tan(v) = 1 and the final equations are given as:
Nxa = Nx + abs(Nxy)
Nya = Ny + abs(Nxy)
Even though the author provides an explanation for taking v = 45 deg, I still just don't understand it. I was hoping that someone with some experience here might be able to offer an alternate explanation. Thank you!
